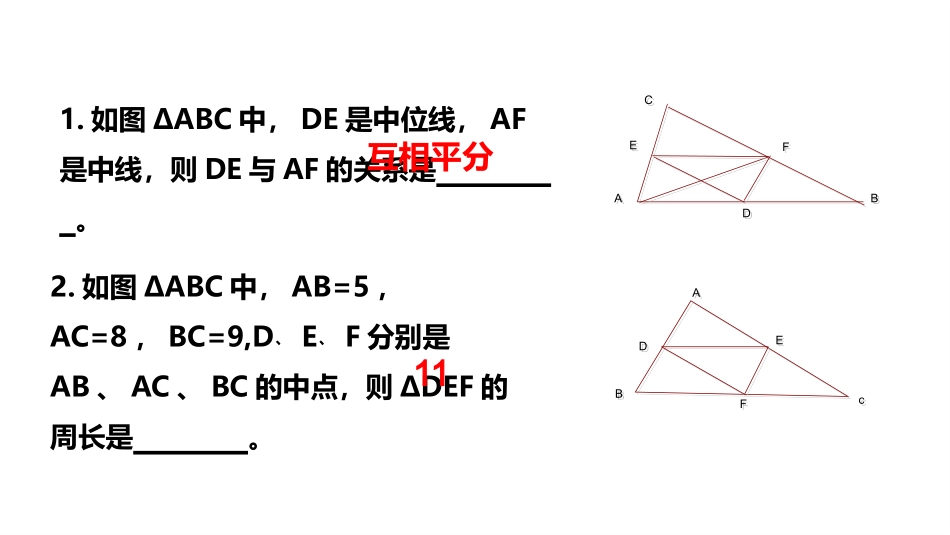
三角形的中位线(中点四边形)1.如图ΔABC中,DE是中位线,AF是中线,则DE与AF的关系是。AACCBBDDEEFF2.如图ΔABC中,AB=5,AC=8,BC=9,D﹑E﹑F分别是AB、AC、BC的中点,则ΔDEF的周长是。FFAABBccDDEE互相平分11ABCDE三角形中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.符号语言:↓↓位置关系大小关系∴DE∥BC,DE=BC12∵在△ABC中,D、E分别为AB、AC的中点例1、如图,任意四边形ABCD中,E,F,G,H分别是AB,BC,CD,AD的中点,四边形EFGH是什么图形?为什么?解:四边形EFGH是平行四边形连接DBAABBCCDDHHEEFFGG∵E、H分别是AB、AD的中点∴EH∥BD,EH=BD12∵F、G分别是CB、CD的中点∴FG∥BD,FG=BD12∴EH∥FG,EH=FG∴四边形EFGH是□发现:①顺次连接任意四边形四边中点所得的四边形是平行四边形。假如把任意四边形改成矩形呢?假如把任意四边形改成菱形呢?②顺次连接矩形的四边中点所得的四边形是菱形。③顺次连接菱形的四边中点所得的四边形是矩形。例2、如图,矩形ABCD中,E,F,G,H分别是AB,BC,CD,AD的中点,四边形EFGH是什么形状?为什么?解:四边形EFGH是菱形连接DB∵E、H分别是AB、AD的中点∴EH∥BD,EH=BD12∵F、G分别是CB、CD的中点∴FG∥BD,FG=BD12∴EH∥FG,EH=FG∴四边形EFGH是□GEDCBAFH∵矩形ABCD∴AC=BD∵E、F分别是AB、BC的中点∴EF=AC12∴四边形EFGH是菱形,AC∴EH=EF例3、如图,菱形ABCD中,E,F,G,H分别是AB,BC,CD,AD的中点,四边形EFGH是什么形状?为什么?解:四边形EFGH是矩形连接DB∵E、H分别是AB、AD的中点∴EH∥BD,EH=BD12∵F、G分别是CB、CD的中点∴FG∥BD,FG=BD12∴EH∥FG,EH=FG∴四边形EFGH是□∵菱形ABCD∴AC⊥BD∴EF⊥BD∵E、F分别是AB、BC的中点∴EF∥ACGEDCBAFH∴四边形EFGH是矩形,AC∴EF⊥FG1、如果顺次连接四边形四边中点所得的四边形是菱形,那么原四边形的两条对角线存在什么关系?讨论:2、上问中的菱形改为矩形呢?3.当四边形满足什么条件时,顺次连接它的四边中点所得的四边形是正方形?(两条对角线相等)(两条对角线相等)(两条对角线垂直)(两条对角线垂直)(两条对角线垂直且相等)(两条对角线垂直且相等)ABDCHEFGABCDEFGHABCDEFGH1.顺次连结矩形四边中点所得的四边形是()A.矩形B.菱形C.正方形D.以上都不对课堂反馈2.如果四边形的对角线互相垂直,那么顺次连结四边形中点所得的四边形是()A.矩形B.菱形C.正方形D.以上都不对3.如果顺次连结四边形各边中点组成的四边形是菱形,那么原来的四边形的对角线()A.互相平分B.互相垂直C.相等D.相等且互相平分BAC4.顺次连结下列各四边形中点所得的四边形是矩形的是()A.平行四边形B.等腰梯形C.矩形D.菱形或对角线互相垂直的四边形D5、如图,在平行四边形ABCD中,E、F分别是BC、AD的中点,AE与BF相交于点G,DE与CF相交于点H,试说明GH∥AD且GH=AD.21GHEFDABCAABBCCDDHHEEFFGGGEDCBAFHGEDCBAFHABDCHEFGABCDEFGHABCDEFGH