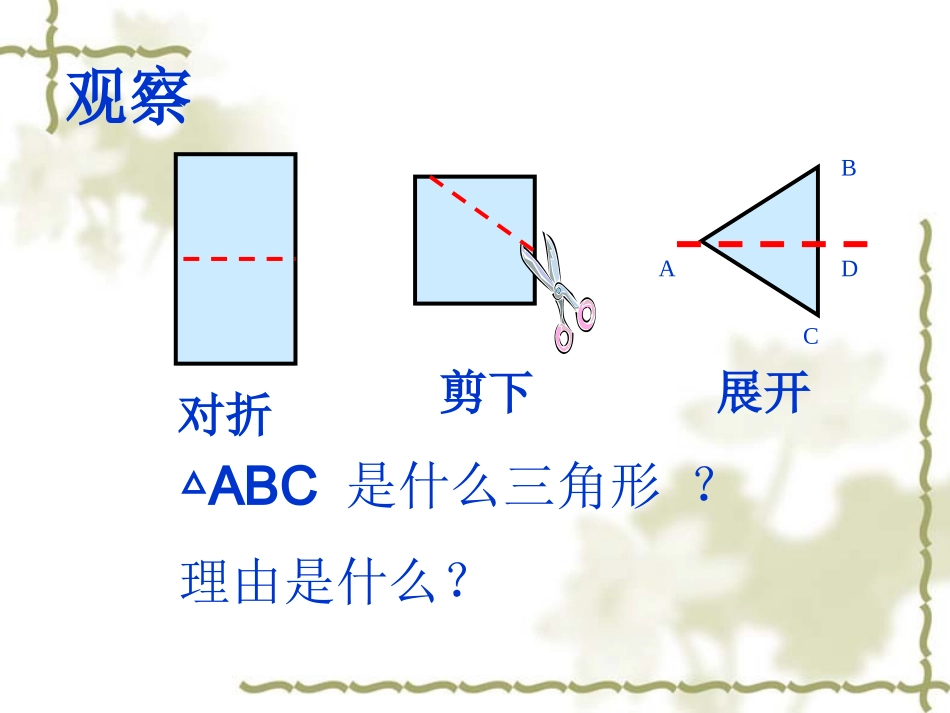
13.3.1等腰三角形的性质讲课教师:高月芳观察对折ACDB展开剪下△ABC是什么三角形?理由是什么?探究ACDB1、把剪出的等腰三角形ABC沿折痕对折,找出重合的线段和角。2、由这些重合的线段和角,你能发现等腰三角形的性质吗?性质1:等腰三角形的两底角相等。(简写成“等边对等角”)CBAABCD⌒⌒12性质2:等腰三角形的顶角的平分线,底边上的中线,底边上的高互相重合。(简称“三线合一”)猜想验证上面的对折重合是否能给你启发?你用什么方法来验证你的猜想?ABCD性质2:等腰三角形的顶角的平分线,底边上的中线,底边上的高互相重合在△ABC中,点D在BC上1、∵AB=AC,ADBC⊥∴∠=∠,____=。2、∵AB=AC,AD是中线,∴⊥,∠=∠。3、∵AB=AC,AD是角平分线,∴⊥,=。112BDDCADBC12ADBCBDDCABCD⌒⌒1212性质1:等腰三角形的两底角相在△ABC中,∵AC=AB()∴∠B=∠C()已知等边对等角CBA表述例1.在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数。应用BCAD解题思路:1、图中相等的角由哪些?2、若设∠A=X,则∠ABD=__,B∠DC=__,C∠=__,ABC∠=__.3、利用三角形内角和可构建方程为:________。1、在等腰△ABC中,AB=AC,∠A=36°,则∠B=——∠C=—2、等腰△ABC中,∠A=50°,则∠B=——,∠C=——巩固3、等腰△ABC中,∠A=120°则∠B=——,∠C=——4、△ABC是等腰直角三角形(AB=AC,∠BAC=90°),AD是底边BC上的高,标出∠B,∠C,∠BAD,∠DAC的度数,图中有哪些相等的线段。BACD5、在△ABC中,AB=AD=DC,∠BAD=26°,求∠B和∠C的度数BDCA巩固等腰三角形的性等腰三角形的性质质等腰三角形等腰三角形三线合一三线合一1、求有关等腰三角形的问题,作顶角平分线、底边中线,底边的高是常用的辅助线;2、熟练掌握求解等腰三角形的顶角、底角的度数;3、掌握等腰三角形三线合一的应用。等边对等角等边对等角这节课你有什么收获?总结谢谢谢谢