2.3.1抛物线的定义与标准方程VIP免费

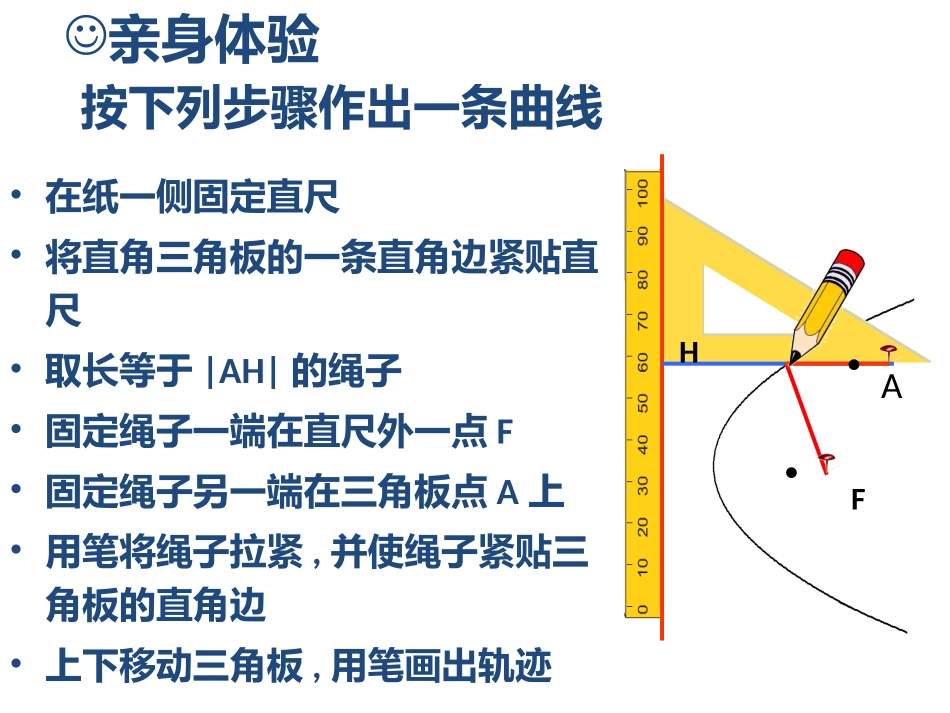
平面上到一定点F和定直线(F不在直线上）距离相等的点的轨迹是什么样的呢？l思考：l•在纸一侧固定直尺•将直角三角板的一条直角边紧贴直尺•取长等于|AH|的绳子•固定绳子一端在直尺外一点F•固定绳子另一端在三角板点A上•用笔将绳子拉紧,并使绳子紧贴三角板的直角边•上下移动三角板,用笔画出轨迹按下列步骤作出一条曲线亲身体验FAH抛物线的生活实例喷泉卫星接收天线彩虹§2.3.1抛物线的定义与标准方程高二（5）班数学组何琴平面内,到一个定点F的距离和定直线l的距离相等的点的轨迹.准线抛物线的定义思考：若定点F在定直线l上，动点P的轨迹是什么？释疑解难P·Fl·dH焦点)(lF复习回顾求椭圆的标准方程的步骤1.建系2.设点3.列式4.化简←充分利用图形的对称性建系←设P(x,y)是椭圆上任意一点←建立关于x,y的关系式←化简x,y的关系式释疑解难试一试：推导抛物线的标准方程P·Fl·dHlxDyoP(x,y)FHddPF关键：释疑解难标准方程：焦点坐标为：准线方程为：)0(22ppxy)0,2(pF2pxlxDyoP(x,y)F问题：若抛物线的开口分别朝左、朝上、朝下，你能根据上述办法求出它的标准方程吗？注意：p的几何意义：焦点到准线的距离.抛物线的标准方程还有哪些形式?分组探究抛物线的标准方程的其它成员其它形式的抛物线的焦点与准线呢？y2=-2px(p>0)x2=2py(p>0)准线方程焦点坐标标准方程图形xFOylxFOylxFOylxFOyly2=2px(p>0))0,2p(2px)0,2p(2px)2p0(，2pyx2=-2py(p>0))2p0(，2py“三看”抛物线的标准方程（1）从方程形式上看：方程左边为二次项，系数为1；右边为一次项，系数为p2四种方程的相同点2p（2）从焦点、准线上看：焦点在对称轴上，准线与对称轴垂直；且原点到焦点与准线的距离相等，均为.(3)从一次项上看：一次项系数为焦点非零坐标的4倍.思考：如何通过抛物线的标准方程，确定焦点的位置和开口方向？注意：一次项定焦点位置一次项系数的正负定开口方向典例分析例1.求下列抛物线的焦点坐标与准线方程.（1）（2）xy42)0(2aaxy典例分析例1.求下列抛物线的焦点坐标与准线方程.（1）（2）xy42)0(2aaxy解：（1）方程具有形式，其中2p=4，p=2,因此焦点坐标为（1，0），准线方程为x=-1.(2)方程可化为,具有标准形式其中p=,因此焦点坐标为（0，),准线方程为y=-pxy2212px2=2pyyax12a21a41a41典例分析例2.求满足下列条件的抛物线的标准方程.（1）焦点为（2）准线方程y=-2)0,2(F[规律方法]1.用待定系数法求抛物线标准方程的步骤求满足下列条件的抛物线的标准方程：(1)准线方程为x＝-2；(2)焦点在y轴上，焦点到准线的距离为5；练习巩固求满足下列条件的抛物线的标准方程：(1)过点（4，-2）课后思考.022)2(上焦点在直线yx