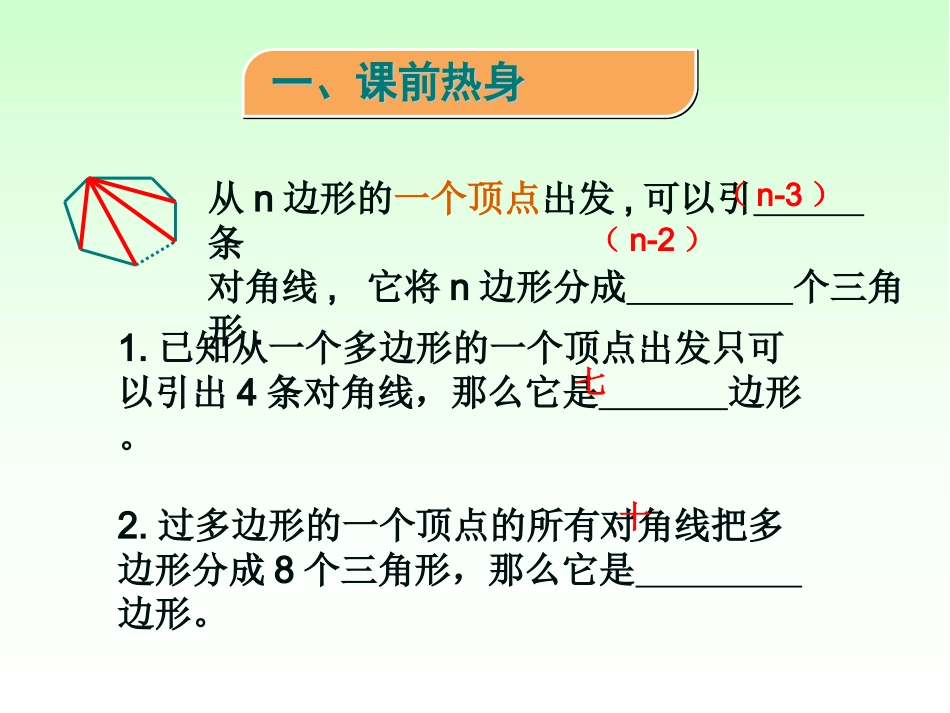
11.3.2多边形的内角和从n边形的一个顶点出发,可以引条对角线,它将n边形分成个三角形.(n-3)(n-2)一、课前热身一、课前热身1.已知从一个多边形的一个顶点出发只可以引出4条对角线,那么它是边形。2.过多边形的一个顶点的所有对角线把多边形分成8个三角形,那么它是边形。七十活动一:你来剪,他来算活动一:你来剪,他来算请取出一张长方形卡纸,任意的剪掉一个角,可以有几种不同的剪法,得到的新多边形是什么?四边形内角和是多少?请说说理由。ABCD活动二:探索多边形的内角和活动二:探索多边形的内角和四边形内角和=2×180°=360°五边形内角和=3×180°=540°ACEDB.这个五边形的内角和应该怎么求呢?活动二:探索多边形的内角和活动二:探索多边形的内角和你能仿照五边形分割成三角形的方法,分割六边形并求其内角和吗?ABCDEF.活动二:探索多边形的内角和活动二:探索多边形的内角和六边形内角和=4×180°=720°内角和三角形个数从一个顶点引出对角线数边数56233×180°=540°............344×180°=720°(n-2)×180°nn-3n-275×180°=900°45快速抢答全品15页12341.五边形的内角和为.2.一个多边形的内角和是720°,则这个多边形的边数是。3.将一个n边形变成(n+1)边形,内角和将。540°6增加180°如果一个四边形的一组对角互补,那么另一组对角有什么关系?ABCD解:如图,四边形ABCD中,∠A+∠C=180°∠A+B+C+D=(4∠∠∠-2)×180°=360°因为∠B+∠D=360°-(∠A+∠C)=360°-180°=180°这就是说:如果四边形一组对角互补,那么另一组对角也互补.所以例1:活动三:探索正多边形的内角活动三:探索正多边形的内角例题:若一个多边形的每一个内角为150°,则这个多边形的边数是多少?例2如图,在六边形的每个顶点处各取一个外角,这些外角的和叫做六边形的外角和.六边形的外角和等于多少?1234ABCDEF56六边形外角和=6×180°-(6-2)×180°=360°外角和=n个平角-内角和=n×180°-(n-2)×180°=360°1.有一个人以左脚为轴旋转一周,这个人转了多少度?2.如果这个人从圆上一点A出发,沿着圆周走,再回到A点时,那么这个人走了多少度?3.如果这个人从六边形的一个顶点A出发,沿六边形走,再回到A点时,那么这个人又走了多少度呢?体现在哪些角上呢?1234ABCDEF56A活动四:探索多边形的外角活动四:探索多边形的外角提升积累谈谈我的收获谈谈我的收获