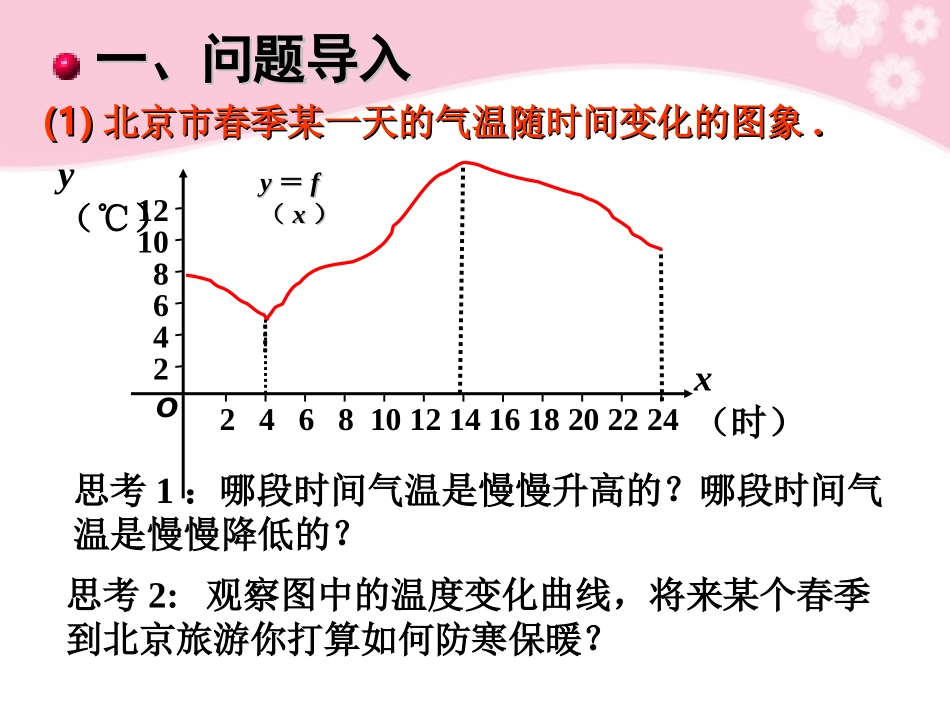
广东省深圳市第三高级中学数学必修一《函数的单调性(1)》课件第第11课时课时(1)(1)北京市春季某一天的气温随时间变化的图象北京市春季某一天的气温随时间变化的图象..思考1:哪段时间气温是慢慢升高的?哪段时间气温是慢慢降低的?一、问题导入一、问题导入思考2:观察图中的温度变化曲线,将来某个春季到北京旅游你打算如何防寒保暖?yy==ff((xx))Ox(时)y(℃)2468101214161820222424681012yxo21()(0)fxxx()≥二、探索新知(一)——增函数二、探索新知(一)——增函数思考思考11::这两个函数的图象分别是什么?二者上升下降的趋势有何共同特征?考查下列两个函数:考查下列两个函数:(2)(2)yy=2=2xx+1+1xxyy思考2:如果一个函数的图象从左至右逐渐上升,那么当自变量x从小到大依次取值时,函数值y的变化情况如何?思考3:如图1为函数f(x)在定义域I内某个区间D上的图象,对于该区间上任意两个自变量x1和x2,当x1x2时,都有f(x1)>f(x2),则函数f(x)在区间D上是增函数还是减函数?y=f(x)xxxx11xx22ff((xx11))f(x2)ooyy图图11探索新知(二)——减函数探索新知(二)——减函数考察下列两个函数:考察下列两个函数:xyoo2()(0)fxxx(1)≤(2)(2)ff((xx)=-2)=-2xx+2+2xxyy思考1:这两个函数的图象分别是什么?它们的上升下降趋势有什么共同特征?如果对于属于定义域I内某个区间D上的任意两个自变量的值x1,x2,当x1<x2时,都有f(x1)>f(x2),那么就说f(x)在这个区间D上是减函数.(如图2)yf(x2)f(x1)x2x10x图2yy==ff((xx))思考3:我们把具有上述特点的函数f(x)称为减函数,那么怎样定义“函数f(x)在区间D上是减函数”?思考2:如图2为函数f(x)在定义域I内某个区间D上的图象,对于该区间上任意两个自变量x1和x2,当x1f>f((xx22)),那么就说,那么就说ff((xx))在这个区间上是减函数在这个区间上是减函数...),1(1)()2(21)()1(.1上是增函数在区间函数在定义域上是减函数函数利用单调性定义证明例xxxfxxf如果函数如果函数yy==ff((xx))某个区间上是增函数或减函数,那某个区间上是增函数或减函数,那么就说函数么就说函数yy==ff((xx))在这一区间上具有(严格的)单调性在这一区间上具有(严格的)单调性..这这一区间叫做函数一区间叫做函数yy==ff((xx))的单调区间的单调区间..此时也说函数此时也说函数yy==ff((xx))在在这一区间上是单调函数这一区间上是单调函数..思考3:函数y=ax2+bx+c(a≠0)在在RR上上是单调函数吗?若不是,那么请写出一个区间,使它在该区间上是单调函数.思考思考11:函数:函数yy==kxkx++bb在在RR上是单调函数吗?上是单调函数吗?探索新知(四)——函数的单调区间探索新知(四)——函数的单调区间?)0()(.2的单调性如何函数思考kxkxf思考4:一般地,若函数f(x)在区间A,B上是单调函数,那么f(x)在区间A∪B上是单调函数吗?例1下图是定义在[-5,5]上的函数y=f(x)的图象,根据图象说出y=f(x)的单调区间,以及在每一单调区间上,y=f(x)是增函数还是减函数.三、知识运用三、知识运用-5O12345-1-2-3-4123-1-2()yfxxy解:y=f(x)的单调区间有[-5,-2),[-2,1),[1,3),[3,5].其中y=f(x)在[-5,-2),[1,3)上是减函数,在[-2,1)...