1.2.3直线与平面的位置关系VIP免费

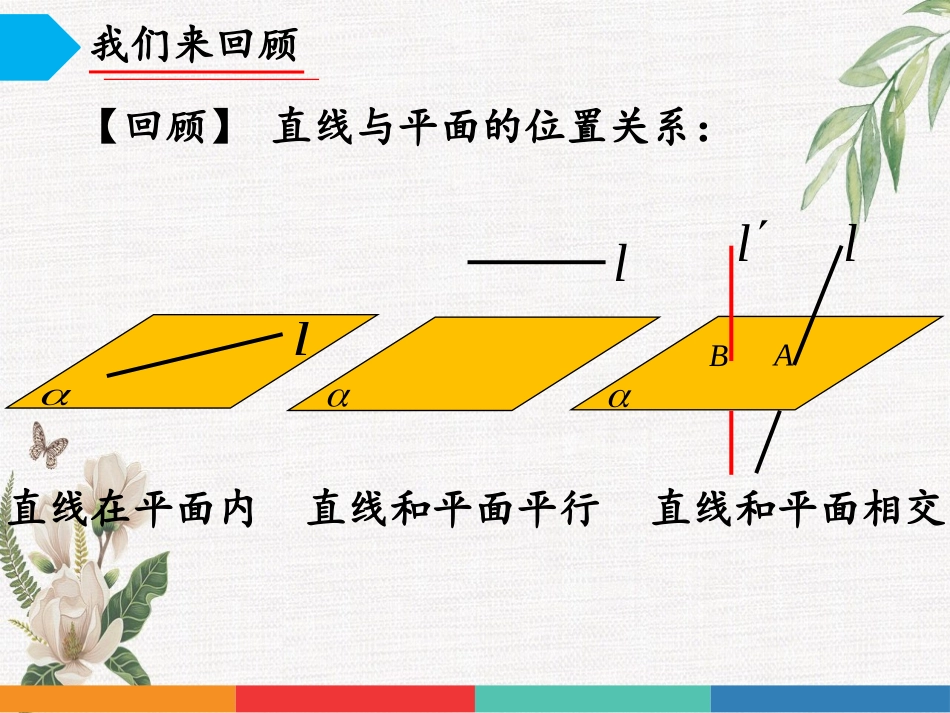
授课人：陈鑫城《普通高中课程标准实验教科书——数学必修（二）》苏教版直线与平面垂直的判定直线和平面平行直线和平面相交直线在平面内llAl我们来回顾Bl【回顾】直线与平面的位置关系：我们来感受生活中有很多直线与平面垂直的实例ABABABABABABABABCC1B1ABα内过点B的直线AB所在直线内不过点B的直线ααAB所在直线内任意一条直线αAB所在直线⊥⊥⊥直线和平面垂直的定义如果一条直线和一个平面相交，并且和这个平面内的任意一条直线都垂直，我们就说这条直线和这个平面垂直.其中直线叫做平面的垂线，平面叫做直线的垂面.交点叫做垂足.A平面的垂线直线的垂面垂足,.llmm任意深入理解“线面垂直定义”判断下列语句是否正确：（若不正确请举反例）1.如果一条直线与一个平面垂直，那么它与平面内所有的直线都垂直.（）2.如果一条直线与平面内无数条直线都垂直，那么它与平面垂直.（）bαa利用定义，我们得到了判定线面垂直的最基本方法，同时也得到了线面垂直的最基本的性质.但是，直接考察直线与平面内所有直线都垂直是不可能的，这就有必要去寻找比定义法更简捷、更可行的直线与平面垂直的方法!,.llmm任意我们来探索小组合作之三角模型秀探索新知：做一做想一想ABCD1.折痕AD与桌面垂直吗？2.如何翻折才能使折痕AD与桌面所在的平面垂直？请同学们拿出一块三角形纸片，我们一起做一个试验：过三角形的顶点A翻折纸片，得到折痕AD，将翻折后的纸片竖起放置在桌面上（BD、DC与桌面接触）ABCD当且仅当折痕AD是BC边上的高时，AD所在直线与桌面所在平面垂直．ABCDABCD2.如何翻折才能使折痕AD与桌面所在的平面垂直？探索新知：我们来发现一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直。即：mαnαm∩n=Bl⊥ml⊥nl⊥α简记:线线垂直线面垂直关键：线不在多，相交则行线面垂直的判定定理lAnmP思考2：判断下列命题是否正确?(1)直线与平面内的两条直线都垂直,则(2)已知直线平面且则b.b,,,abc,,,,abacb,bcP.a我们来应用【例题】在正方体AC1中,O为下底面的中心,(1)求证：AC⊥面D1B1BD(2)求证：AC⊥D1OABDCA1B1D1C1O我们来巩固1如图，在四棱锥中P﹣ABCD，底面ABCD为菱形，∠BAD=60°，Q为AD中点，△PAD是正三角形．（1）求证：AD⊥平面PQB；我们来巩固2在如图所示的几何体中，面CDEF为正方形，面ABCD为等腰梯形，AB∥CD，，AB=2BC=2，AC⊥FB．（Ⅰ）求证：AC⊥平面FBC；我们来巩固3如图，PA垂直与圆O所在的平面，AB是圆O的直径，C是圆周上任意一点，过A作AE⊥PC于点E,求证：AE⊥平面PBC.PABCOE我们来小结空间问题平面问题线线垂直线面垂直（1）本节课你学会了哪些判断直线与平面垂直的方法？请用自己的语言表述。（2）直线与平面垂直的判定定理中体现了那些数学思想方法？定理定义1.定义2.定理我们来小结（3）重点总结：证明线线垂直的方法有哪些？①勾股定理的逆定理（已知长度）②等腰三角形的三线合一③利用线面垂直的性质④正方形、菱形的对角线互相垂直⑤直径所对的圆周角是90°生活现象数学知识抽象（核心素养）生活运用模型作业Homework推理我们共提高1.（选做）探究直线与平面垂直的性质2.（校本）查阅资料，了解直线与平面垂直的判定定理的证明过程.谢谢