第3讲等比数列及其前n项和学案完成1VIP免费

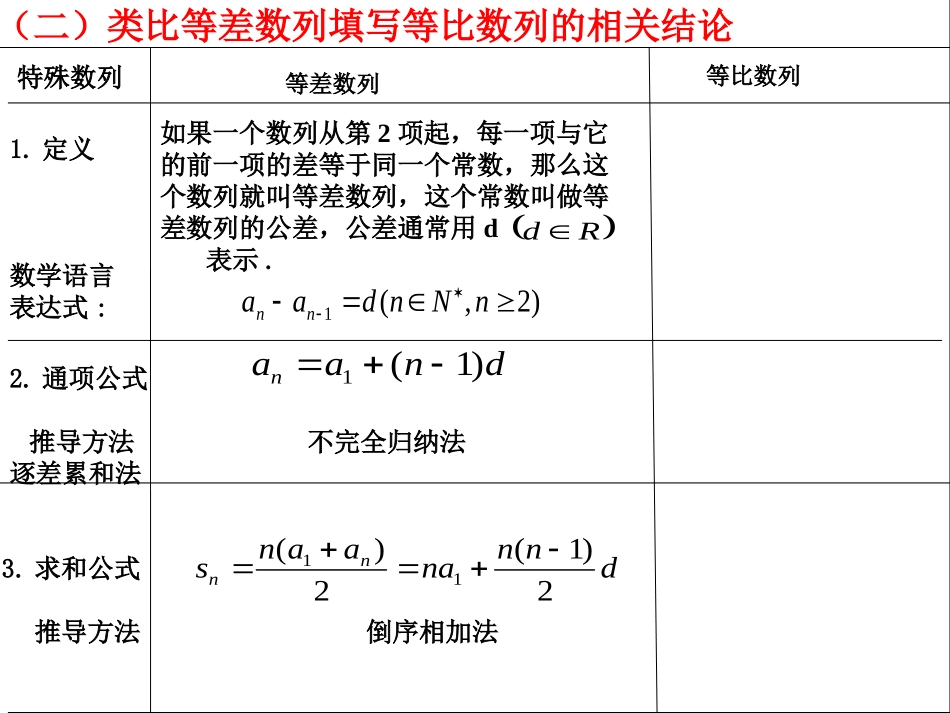
（一）学习目标：1.深刻理解等比数列的定义,会证明一个数列是等比数列.2.掌握等比数列的通项公式与前n项和公式,并会应用两个基本量进行相关计算.3.掌握等比数列的性质并会灵活应用,能解决一些等比数列的综合问题.（二）类比等差数列填写等比数列的相关结论)2,(1nNndaanndnaan)1(1dnnnaaansnn2)1(2)(11Rd特殊数列等差数列等比数列1.定义数学语言表达式:如果一个数列从第2项起，每一项与它的前一项的差等于同一个常数，那么这个数列就叫等差数列，这个常数叫做等差数列的公差，公差通常用d表示.2.通项公式推导方法不完全归纳法逐差累和法3.求和公式推导方法倒序相加法特殊数列等差数列等比数列4.常用性质),,,(2,2,)3(Nnmqpaaamqpaaaanmqpmqpnmqp则有若则有若).(...,,)4(232NmSSSSSmmmmm等差数列也是),()()2(Nnmdmnaadmnaamnmn或.)2,,.2,,,)1(成立的充要条件成等差数列是（等差中项且的叫做成等差数列，则若baAbAabaAbaAbAa辨析感悟：..23,321)3(.,,)2(2nnnnaSSaacbcba则的前项和为的等比数列，公比为设首项为是成等比数列的充要条件三个数.,112仍是等比数列是等比数列，则）如果（nnaaanaaaSaaannnnn1)1()4(，则其前项和为通项公式是数列.)5(812484成等比数列，，为等比数列，则数列SSSSSan题型一等比数列基本量求解.322,)1(131212项和的首项、公比及前等差中项，求数列的和为且中在等比数列、例naaaaaaann211或213,3,11nnSqa.,21,7)2(33的值公比则前三项和中，在等比数列qSaan.3,,,,1,,,的值成等比数列，则若变式训练：已知xyzzyxRzyx33.,21,7)2(33的值公比则前三项和中，在等比数列qSaan7211)1(1213313qaaqqaSq时解：当21)1(1)1)(1(21213qqaqqqqaS3122qqq题型二等比数列的判定与证明.,),2(3231,23211是等比数列并证明数列，求且中、已知数列例naaaNnnnaaaannnn15,43223312aaa解：,nabnn证明：令)()2(1无关的非零常数是与定义法：即证nqnqbbnn132311nannann3)2()1(11nnanabbnnnn则.3211为公比的等比数列为首项，是以为所以anan.,1,是等比数列求证设，有任意的，且对的前项和为变式训练：已知数列nnnnnnnbabnSaNnSa题型三等比数列性质的应用-749.,21,72.,8,2136421016574的值求项和，的前是等比数列）已知（的值则为等比数列，）已知（例SSSnaSaaaaaaannn成等比数列46242,,SSSSS211)1(71)1((414212qqaSqqaS方法二）解311142qq231)1)(1(12222qqqqqqaS1)1(616整体代入法.,21,72642的值求项和，的前是等比数列）已知（SSSnaSnn711qa491])(1[321qqa736223532,12,12aaaaaaaan则中，的等比数列变式：在各项均为正数8小结：1.等比数列的定义：2.等比数列的通项公式：3.等比数列求和公式：an=a1qn-14.等比数列性质：,11111qqaaqqannnS,1na(q=1).(q≠1).{推导方法：错位相减法5.等比数列运算中注意的问题：方程思想、整体代入、分类讨论的数学思想。)0)(2(1qnqaann课后作业：1.整理本节课内容2、完成练习册第80页～82页