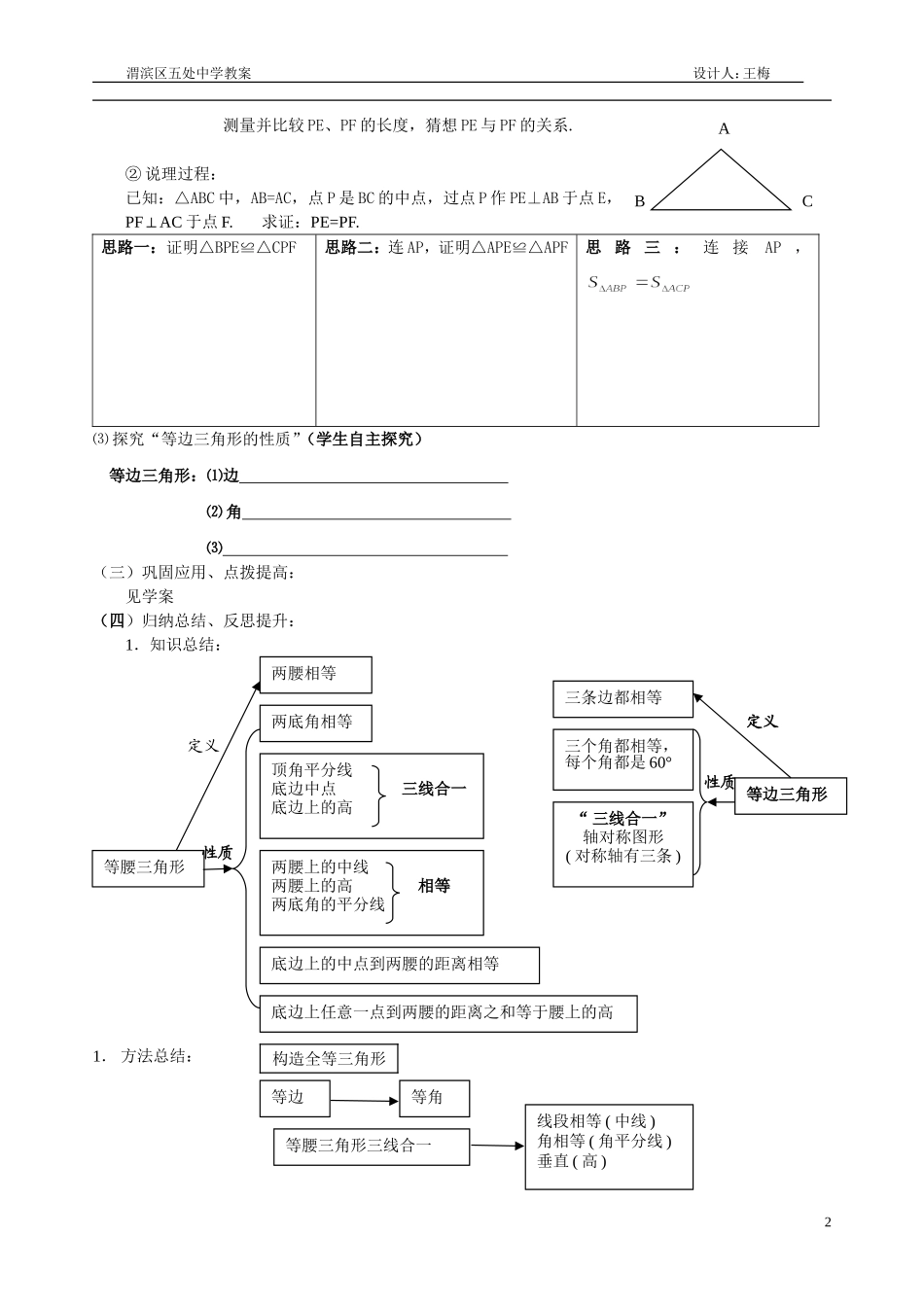
渭滨区五处中学教案设计人:王梅1.1等腰三角形(二)学生知识现状1.八上《平行线的证明》学生已经感受了证明的必要性,并通过平行线有关命题的证明过程,了解了一些基本的证明方法和规范,积累了一定的证明的经验;2.七下,学生已经探索得到了有关三角形全等和等腰三角形的有关命题;目标1.进一步了解掌握等腰三角形的性质,并能灵活运用解决实际问题;2.经历“探索——发现——猜想——证明”的过程,能够用综合法证明等腰三角形中特殊线段的有关性质,通过独立思考,交流讨论,发展学生推理能力和用数学语言进行规范的表达的能力;3.通过活动,使学生养成乐于观察生活、乐于学习、乐于探索的精神,养成用数学的思维思考问题的习惯;重点探索证明等腰三角形中特殊线段的性质,掌握证明的基本要求和方法.难点从实践中得出结论,并用数学方法证明其正确性,并能用数学语言规范书写证明过程.一、知识回顾、导入新课:知识回顾:⑴什么叫等腰三角形:⑵等腰三角形的性质定理:导入新课:等腰三角形是一种特殊的三角形,今天我们继续探究等腰三角形的特殊线段之间的关系.二、自主学习,合作探究1.自主学习:等腰三角形能做出哪些特殊线段?高、中线、角平分线⑵动手操作:等腰三角形的高、中线、角平分线之间有什么关系?⑶合理猜想:①等腰三角形两腰的中线;②等腰三角形两腰上的高;③等腰三角形两底角的角平分线;④等腰三角形;⑤等腰三角形.2.合作探究:⑴探究“等腰三角形两腰上的相等”(在上述猜想①-③中任选一个进行证明)详见学案思考:你还有其他结论吗?①等腰三角形两腰的中线相等;②等腰三角形两腰的高相等;③等腰三角形两底角的平分线相等;⑵探究“等腰三角形底边上的中点到两腰的距离相等”.①动手操作:在等腰△ABC的取底边BC的中点P,过点P作PE⊥AC于点E,PF⊥AB于点F.1渭滨区五处中学教案设计人:王梅测量并比较PE、PF的长度,猜想PE与PF的关系.②说理过程:已知:△ABC中,AB=AC,点P是BC的中点,过点P作PE⊥AB于点E,PFAC⊥于点F.求证:PE=PF.思路一:证明△BPE≌△CPF思路二:连AP,证明△APE≌△APF思路三:连接AP,⑶探究“等边三角形的性质”(学生自主探究)等边三角形:⑴边⑵角⑶(三)巩固应用、点拨提高:见学案(四)归纳总结、反思提升:1.知识总结:1.方法总结:2等腰三角形两腰相等两底角相等顶角平分线底边中点三线合一底边上的高两腰上的中线两腰上的高相等两底角的平分线底边上的中点到两腰的距离相等底边上任意一点到两腰的距离之和等于腰上的高定义性质等边三角形定义性质三条边都相等三个角都相等,每个角都是60°“三线合一”轴对称图形(对称轴有三条)等边等角等腰三角形三线合一线段相等(中线)角相等(角平分线)垂直(高)ABC构造全等三角形