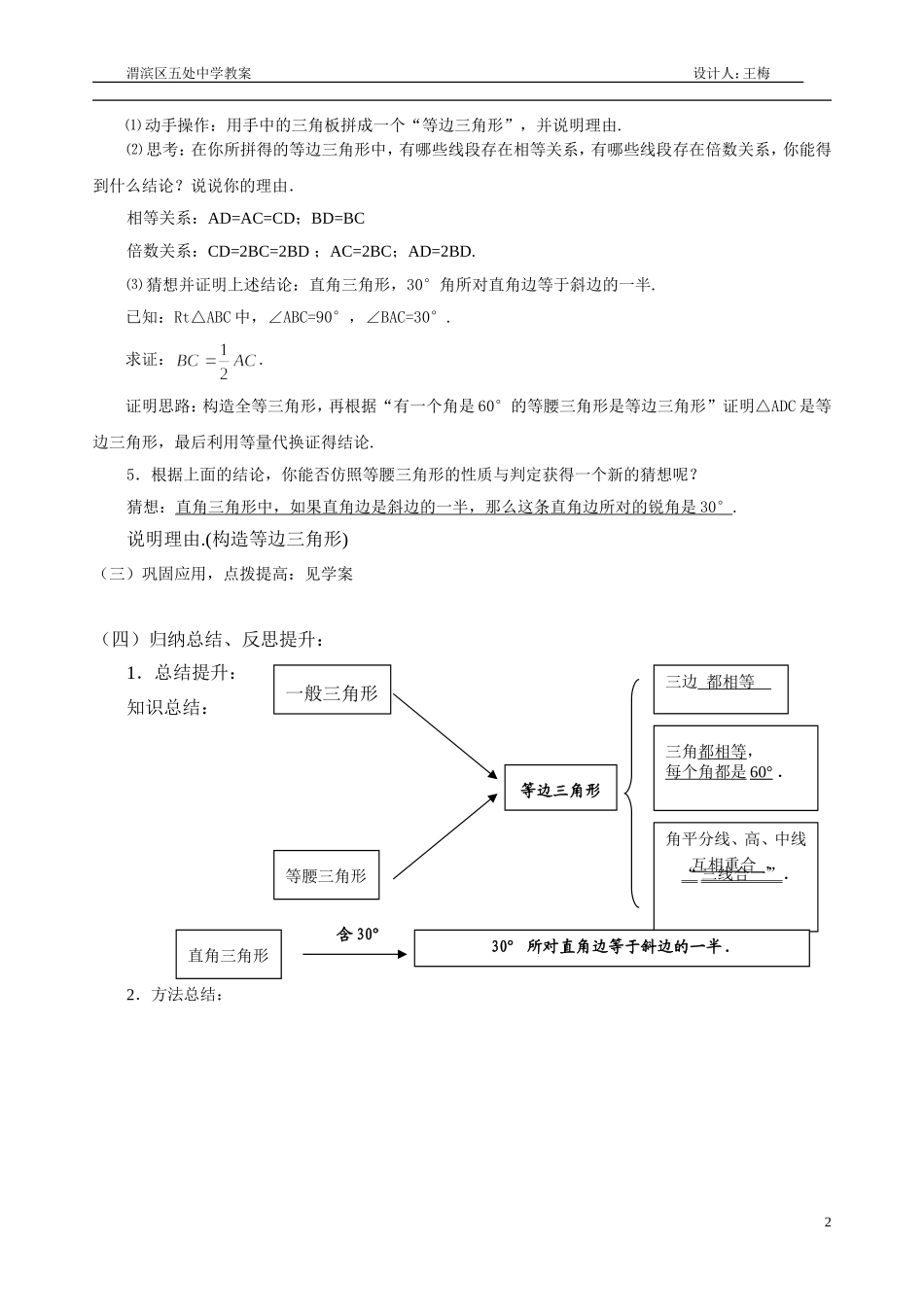
渭滨区五处中学教案设计人:王梅1.1等腰三角形(四)学生知识现状学生已经掌握了全等三角形、等腰三角形相等关系知识在前两节课,学生已经经历了独立探索发现定理的过程,并能基本规范地证明相关命题,这些都为本节课进一步探索发现相关定理提供了较好的知识基础和活动经验基础。目标1.理解等边三角形的判定条件及其证明,理解含30º角的直角三角形性质及其证明,并能利用这两个定理解决一些简单的问题;2.经历实际操作,探索含有30º角的直角三角形性质及其推理证明过程,发展合情推理能力和初步的演绎推理的能力;3.经历运用几何符号和图形描述命题的条件和结论的过程,建立初步的符号感,发展抽象思维;4.在具体问题的证明过程中,有意识地渗透分类讨论、逆向思维的思想,提高学生的能力.5.在探究过程中,引导学生积极参与数学学习活动,在活动中获得成功的体验,锻炼克服困难的意志,建立自信心.重点探索等边三角形判定定理及含30°角的直角三角形的性质定理的发现与证明.难点含30°角的直角三角形性质定理的探索与证明.学具两个含30°角的三角板一、提出问题,导入新课:回顾等腰三角形的性质与判定方法,那么等边三角形作为一种特殊的等腰三角形,具有哪些更特殊的性质呢?我们又如何去判定一个三角形是等边三角形呢?二、自主学习:1.探究“等边三角形的判定”(条件:一般三角形)⑴学生自主探究:一般三角形满足什么条件则得等边三角形,引导学生从边和角两个方面进行研究.⑵交流汇报:①三边相等的三角形(定义);②三个角都相等的三角形是等边三角形(由等角对等边得).2.探究“等边三角形的判定”(条件:等腰三角形)⑴学生自主活动,探究具有什么条件的等腰三角形是等边三角形.(引导学生从边的条件和角的条件进行分析)⑵交流汇报:①从“边”着手研究:底=腰,则得.等同于“三边相等”.②从“角”着手研究:如果等腰三角形三个角都是60°,则得.提出问题:一方面,三个角都是60°,即三个角相等;另一方面,这个条件可以少不?两个角?一个角?③从“角”着手研究:如果等腰三角形一个顶角是60°,所得三角形是等边三角形.④从“角”着手研究:如果等腰三角形一个底角是60°,所得三角形是等边三角形.⑶形成结论:有一个角是60°的等腰三角形是等边三角形.(重点理解两个条件)⑷说理:分两种情况讨论:①顶角是60°的等腰三角形.②底角是60°的等腰三角形.方法总结:已知等腰的一个内角,要进行分类讨论.已知角是钝角或直角,这个角是等腰三角形的顶角.已知角是锐角,这个角可能是顶角,也可能是底角.3.等边三角形的性质与判定区别:联系:4.直角三角形的性质:1ADCB渭滨区五处中学教案设计人:王梅⑴动手操作:用手中的三角板拼成一个“等边三角形”,并说明理由.⑵思考:在你所拼得的等边三角形中,有哪些线段存在相等关系,有哪些线段存在倍数关系,你能得到什么结论?说说你的理由.相等关系:AD=AC=CD;BD=BC倍数关系:CD=2BC=2BD;AC=2BC;AD=2BD.⑶猜想并证明上述结论:直角三角形,30°角所对直角边等于斜边的一半.已知:Rt△ABC中,∠ABC=90°,∠BAC=30°.求证:.证明思路:构造全等三角形,再根据“有一个角是60°的等腰三角形是等边三角形”证明△ADC是等边三角形,最后利用等量代换证得结论.5.根据上面的结论,你能否仿照等腰三角形的性质与判定获得一个新的猜想呢?猜想:直角三角形中,如果直角边是斜边的一半,那么这条直角边所对的锐角是30°.说明理由.(构造等边三角形)(三)巩固应用,点拨提高:见学案(四)归纳总结、反思提升:1.总结提升:知识总结:2.方法总结:2等边三角形一般三角形等腰三角形三边都相等三角都相等,每个角都是60°.角平分线、高、中线互相重合,“三线合一”.直角三角形含30°30°所对直角边等于斜边的一半.