1.1.3导数的几何意义VIP免费

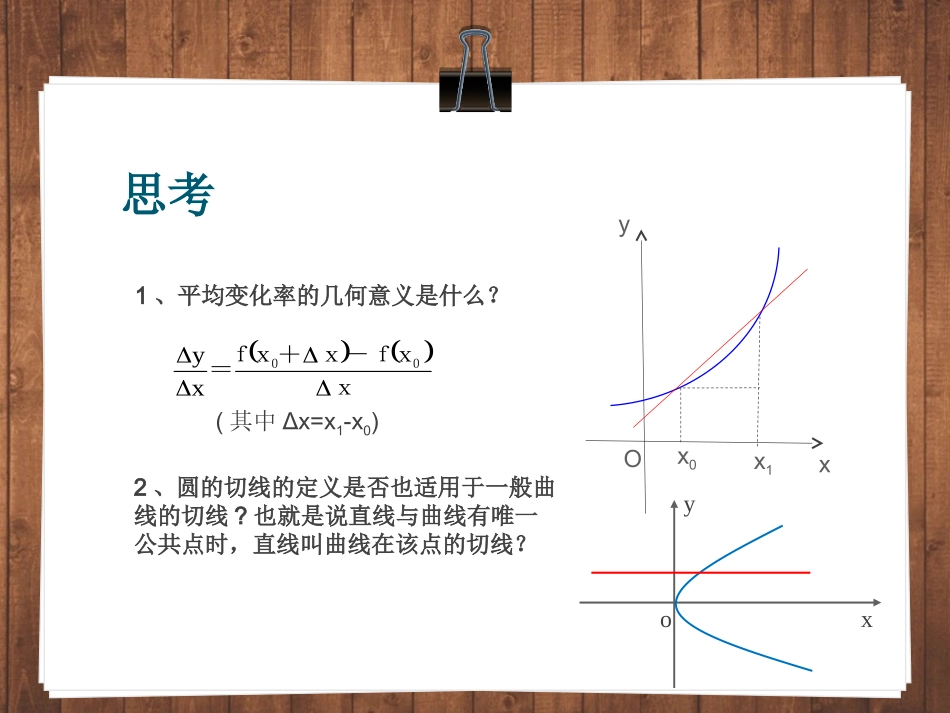
STAR导数的几何意义导数的几何意义庄河高级中学田宇复习1、圆的切线定义2、平均变化率的公式3、瞬时变化率（导数）的公式思考1、平均变化率的几何意义是什么？Oxyx0x1ｘｘ－ｆｘ＋ｘｆ＝００xy(其中Δx=x1-x0)2、圆的切线的定义是否也适用于一般曲线的切线?也就是说直线与曲线有唯一公共点时，直线叫曲线在该点的切线？xyoP1P2P3P4PTTTTPPxfyxfyxfyxfyOyxOyxOyxOyx1234?,,4,3,2,1,,00什么是趋势化变的割线时趋近于点沿着曲线当点如图nnnnPPxfxPxfnxfxPPQoxyy=f(x)割线切线T观察当点Q沿着曲线逐渐向点P接近时,割线PQ绕着点P逐渐转动的情况.我们发现,当点Q沿着曲线无限接近点P即Δx→0时,割线PQ如果有一个极限位置PT.则我们把直线PT称为曲线在点P处的切线.探究一：导数的几何意义?•函数在x0处的导数的几何意义:曲线y=f(x)在(x0,f(x0))点处的导数等于切线的斜率即:这个概念:①提供了求曲线上某点切线的斜率的一种方法;②切线斜率的本质——函数在x=x0处的导数.例1求曲线y=x2+1（1）在P(1,2)点处的切线方程。（2）过Q(1,1)点的切线方程。例2求曲线y=x3过点(1,1)的切线方程。探究二：如何利用导数的几何意义来求切线方程？求切线方程应当注意什么？