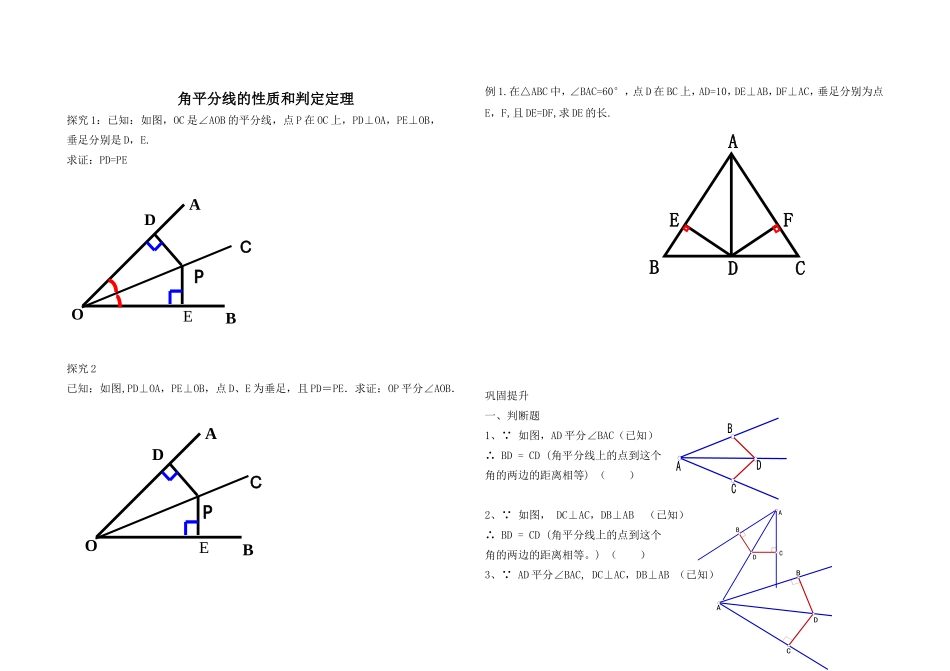
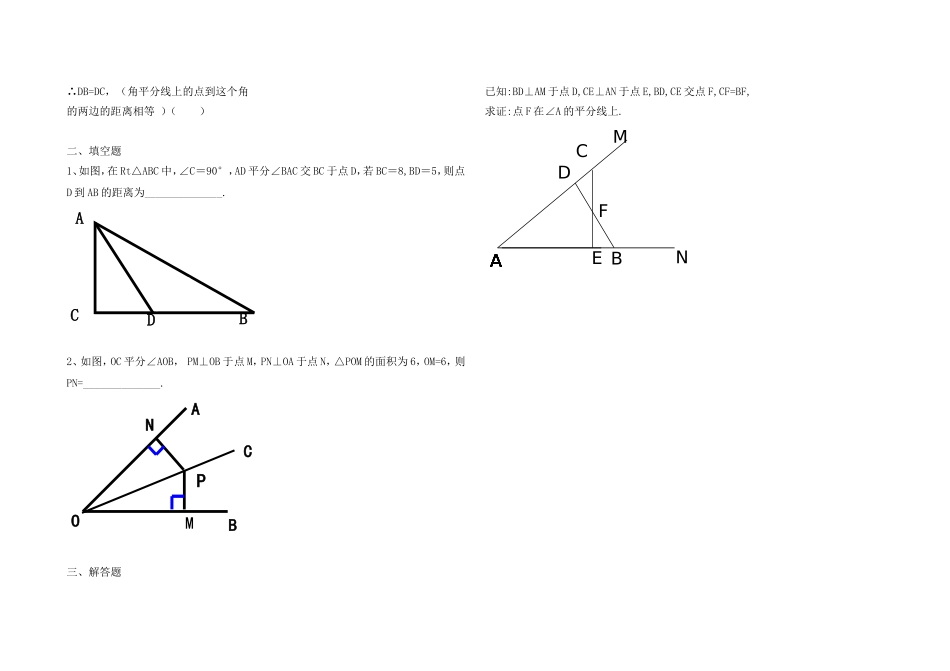
角平分线的性质和判定定理探究1:已知:如图,OC是∠AOB的平分线,点P在OC上,PD⊥OA,PE⊥OB,垂足分别是D,E.求证:PD=PE探究2已知:如图,PD⊥OA,PE⊥OB,点D、E为垂足,且PD=PE.求证:OP平分∠AOB.例1.在△ABC中,∠BAC=60°,点D在BC上,AD=10,DE⊥AB,DF⊥AC,垂足分别为点E,F,且DE=DF,求DE的长.巩固提升一、判断题1、∵如图,AD平分∠BAC(已知)∴BD=CD(角平分线上的点到这个角的两边的距离相等)()2、∵如图,DC⊥AC,DB⊥AB(已知)∴BD=CD(角平分线上的点到这个角的两边的距离相等。)()3、∵AD平分∠BAC,DC⊥AC,DB⊥AB(已知)DPEAOBCEAOBDPCABCDEFADCBADCBADCB∴DB=DC,(角平分线上的点到这个角的两边的距离相等)()二、填空题1、如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D,若BC=8,BD=5,则点D到AB的距离为______________.2、如图,OC平分∠AOB,PM⊥OB于点M,PN⊥OA于点N,△POM的面积为6,OM=6,则PN=______________.三、解答题已知:BD⊥AM于点D,CE⊥AN于点E,BD,CE交点F,CF=BF,求证:点F在∠A的平分线上.ACDBMAOBNPCADNEBFMCA