特殊角的三角函数值及用计算器求角的三角函数值-(2)VIP免费

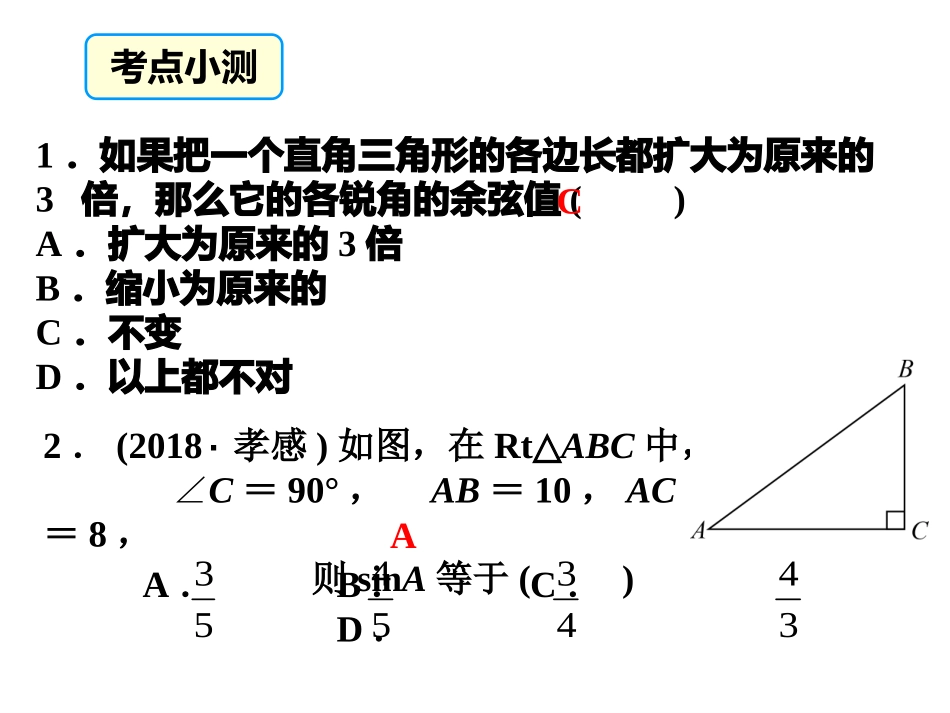
知识回顾问题探究讲授新课当堂练习九年级数学下教学课件28.1锐角三角函数第二十八章锐角三角函数第3课时特殊角的三角函数值课堂小结复习ABC∠A的邻边∠A的对边斜边知识回顾1.说出角A的锐角三角函数ABC∠B的对边∠B的邻边斜边2.变式训练：说出角B的三角函数3.互余的两角之间的三角函数关系：若∠A+∠B=90°，则sinAcosB，cosAsinB，tanA·tanB=.==11．如果把一个直角三角形的各边长都扩大为原来的3倍，那么它的各锐角的余弦值()A．扩大为原来的3倍B．缩小为原来的C．不变D．以上都不对C2．(2018·孝感)如图，在Rt△ABC中，∠C＝90°，AB＝10，AC＝8，则sinA等于()A．B．C．D．53544334A考点小测4．(2015·丽水)如图，点A为∠α边上的任意一点，过点A作AC⊥BC于点C，过点C作CD⊥AB于点D，下列用线段比表示cosα的值，错误的是()A．BDBCB．BCABC．ADACD．CDACC3．(2016·广东)如图，在平面直角坐标系中，点A的坐标为(4，3)，那么cosα的值是()A．34B．43C．35D．45D考点小测问题探究探究:30°、45°、60°角的三角函数值分别是多少？合作探究如图，分别在含30°角和45°角的直角三角形中，设较短边长为1，利用勾股定理和三角函数定义填空：30°60°CAB45°45°CBA30sin30cos30tan60sin60cos____60tan45sin45cos____45tan重点知识★运用旧知，归纳结果30°45°60°sinαcosαtanα1222323222123313sinα与tanα，角度越大，函数值越；对于cosα，角度越大，函数值越.大小1，2，3;3,2,1;3，9，27。弦比2，切比3，分子根号别忘添。归纳重点知识★例3求下列各式的值：（1）cos260°+sin260°．（2）45tan45sin45cos解：（1）cos260°+sin260°222321＝1（2）45tan45sin45cos12222＝0典例精析提示：cos260°表示(cos60°)2，(cos60°)×(cos60°).讲授新课1.cos3023322（天津中考）的值等于（）A.B.C.1D.2.(2018.1322大庆中考）2cos60等于（)A.1B.C.D.23.(60cos60tan45_____大庆中考）计算：sin当堂练习BA41(P67)1.求下列各式的值：（1）1－2sin30°cos30°（2）3tan30°－tan45°+2sin60°（3）60tan)30sin30(cos22解：强化练习当堂练习131222312（1）原式3331232313231（2）原式3])21()23[(22313（3）原式例4.（1）如图，在Rt△ABC中，∠C=90°，AB=，BC=，求∠A的度数．（2）如图，已知圆锥的高AO等于圆锥的底面半径OB的倍，求．336解：2263sin)1(ABBCA45A33tan)2(OBOBOBAOa60a点拨：要想求一个锐角的大小，只需求出其三角函数值即可.典例精析重点知识★讲授新课4.(2018.,2tan1,sin,2ABCABABABC南关校级一模）在中，都是锐角，对最确切的判断是（）A.等腰三角形B.等腰直角三角形C.直角三角形D.锐角三角形当堂练习B当堂练习755．(2014·本溪)在△ABC中，∠B＝45°，cosA＝12，则∠C的度数是________．75°26.1sin(tan1)02________（酒泉中考）已知，均为锐角，且满足则度(P67)2.在Rt△ABC中，∠C＝90°，求∠A、∠B的度数．21,7ACBCBAC721强化练习当堂练习解：∴∠A=30°∴∠B=90°－∠A=90°－30°=60°3331217tanACBCA90C点拨：要想求一个锐角的大小，只需求出其三角函数值即可.（1）特殊角的三角函数值：30°45°60°sinαcosαtanα1222323222123313（2）若角α为锐角，则随角α的增大，正弦(sinα)______，余弦(cosα)______，正切(tanα)______.（3）若角α为锐角，则_____cosα>_____，tanα>____.逐渐增大逐渐减小逐渐增大01001知识梳理课堂小结重难点突破策略课堂小结（1）锐角三角函数的基本计算和求锐角大小，准确记忆特殊角的三角函数值是关键.（2）解决与三角函数有关的问题需要有基本图形------直角三角形。如果没有直角三角形时，可添加辅助线构造直角三角形。