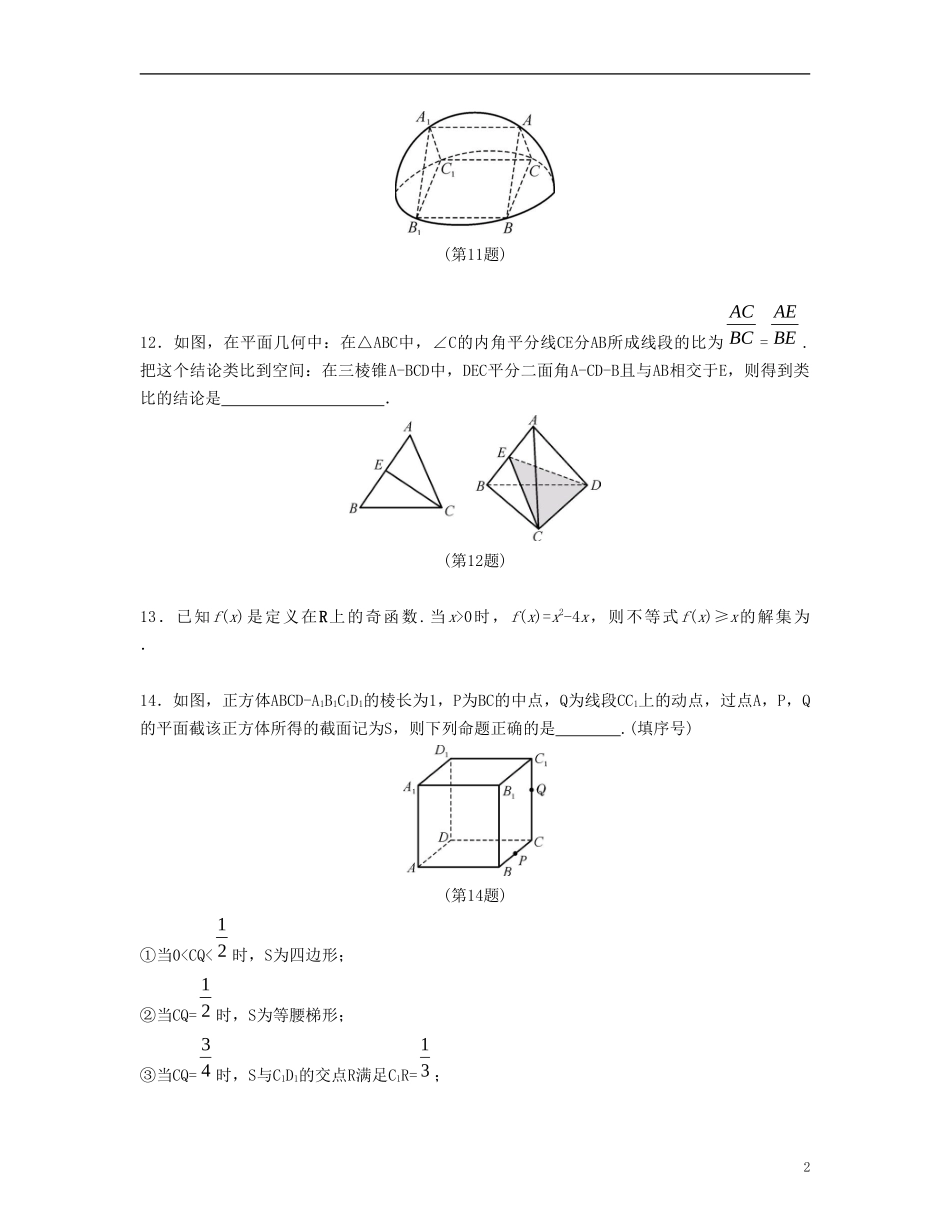
阶段训练三一、填空题1.设a,b∈[0,+∞),A=a+b,B=ab,则A,B的大小关系是.2.在数列{an}中,若a1=a2=1,且an+2-an=1,则数列{an}的前30项和为.3.函数f(x)=log2(x2+2x-3)的定义域是.4.若正三棱锥的底面边长为2,侧棱长为1,则此三棱锥的体积为.5.已知数列{an}为等差数列,Sn为其前n项和,若a7-a5=4,a11=21,Sk=9,则k=.6.若不等式x2+ax-2>0在区间[1,5]上有解,则实数a的取值范围是.7.在数列{an}中,已知a1=1,a2=2,an+1=an+an+2(n∈N*),那么a7=.8.设n为正整数,f(n)=1+12+13+…+1n,计算得f(2)=32,f(4)>2,f(8)>52,f(16)>3,观察上述结果,可推测一般的结论为9.设O为坐标原点,点A114,,若M(x,y)满足不等式组212xyxy,,,则OM�·OA�的最小值是.10.假设平面α∩平面β=EF,AB⊥α,CD⊥β,垂足分别为B,D,如果增加一个条件,就能推出BD⊥EF,现有下面四个条件:①AC⊥α;②AC与α,β所成的角相等;③AC与BD在β内的射影在同一条直线上;④AC∥EF.其中能成为增加条件的是.(填序号)11.如图,直三棱柱ABC-A1B1C1的六个顶点都在半径为1的半球面上,AB=AC,侧面BCC1B1是半球底面圆的内接正方形,则侧面ABB1A1的面积为.1(第11题)12.如图,在平面几何中:在△ABC中,∠C的内角平分线CE分AB所成线段的比为ACBC=AEBE.把这个结论类比到空间:在三棱锥A-BCD中,DEC平分二面角A-CD-B且与AB相交于E,则得到类比的结论是.(第12题)13.已知f(x)是定义在R上的奇函数.当x>0时,f(x)=x2-4x,则不等式f(x)≥x的解集为.14.如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S,则下列命题正确的是.(填序号)(第14题)①当00恒成立,求实数x的取值范围.318.某市近郊有一块大约500m×500m的接近正方形的荒地,地方政府准备在此建一个综合性休闲广场,首先要建设如图所示的一个总面积为3000m2的矩形场地,其中阴影部分为通道,通道宽度为2m,中间的三个矩形区域将铺设塑胶地面作为运动场地(其中两个小场地形状相同),塑胶运动场地占地面积为Sm2.(1)分别用x表示y和S的函数关系式,并给出定义域;(2)怎样设计能使S取得最大值,并求出最大值.(第18题)19.如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.(1)若PA=PD,求证:平面PQB⊥平面PAD;(2)令点M在线段PC上,PM=tPC,试确定实数t的值,使PA∥平面MQB.(第19题)20.已知等差数列{an}满足a3=7,a5+a7=26.(1)求数列{an}的通项公式;(2)若m=222nan,数列{bn}满足关系式bn=-1112nnbmn,,,,求证:数列{bn}的通项公式为bn=2n-1;(3)设(2)中的数列{bn}的前n项和为Sn,对任意的正整数n,(1-n)·(Sn+n+2)+(n+p)2n+1<2恒成立,求实数p的取值范围.【阶段训练答案】4阶段训练三1.A≥B【解析】由题意得,B2-A2=-2ab≤0,且A≥0,B≥0,可得A≥B.2.240【解析】由题意可知,数列a1,a3,a5,…,a29和数列a2,a4,…,a30均是以1为首项,1为公差的等差数列,所以S30=(a1+a3+…+a29)+(a2+a4+…+a30)=2×151411512=240.3.(-∞,-3)∪(1,+∞)【解析】由x2+2x-3>0(x+3)(x-1)>0,解得x<-3或x>1.4.16【解析】如图...