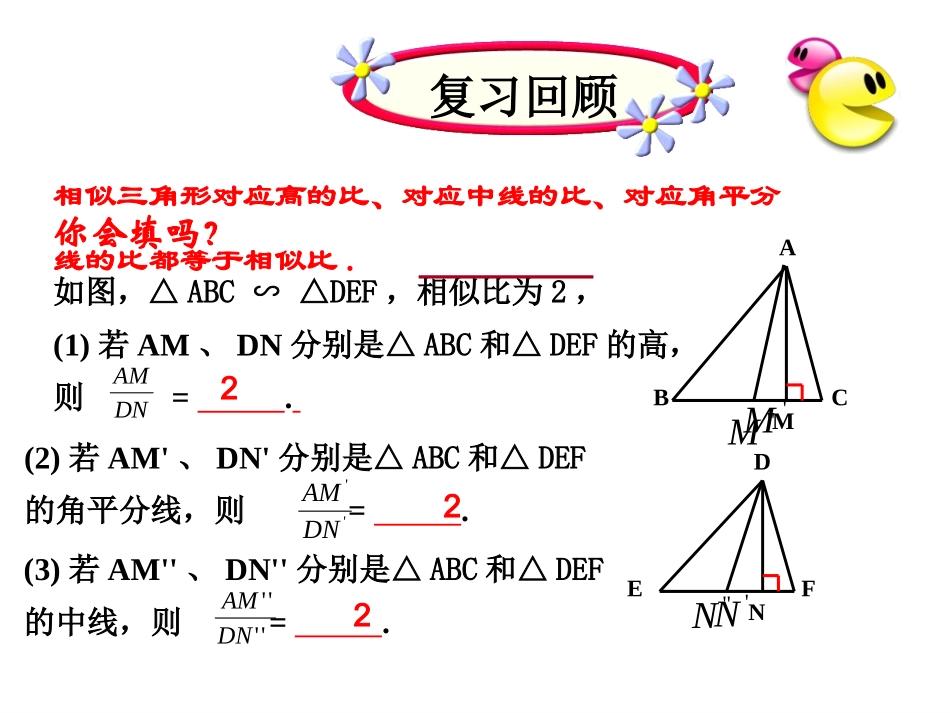
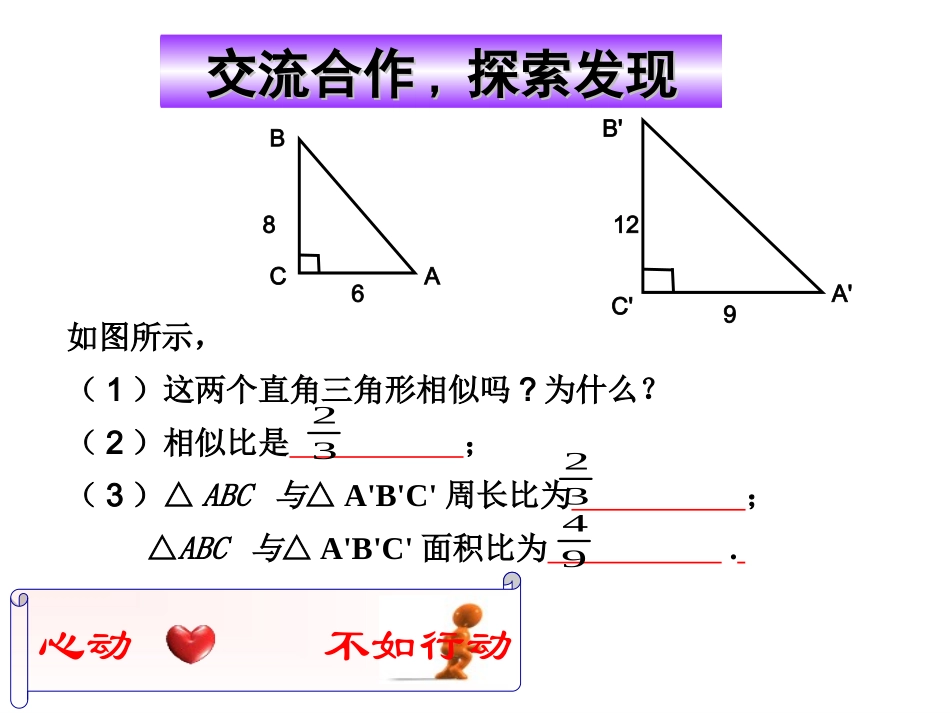
2.7.2相似三角形的性质复习回顾你会填吗?如图,△ABC∽△DEF,相似比为2,(1)若AM、DN分别是△ABC和△DEF的高,则=.ABCMDEFNDNAM2(2)若AM'、DN'分别是△ABC和△DEF的角平分线,则=.'M'N''DNAM2''M''N(3)若AM''、DN''分别是△ABC和△DEF的中线,则=.''''DNAM2相似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比.交流合作交流合作,,探索发现探索发现心动不如行动如图所示,(1)这两个直角三角形相似吗?为什么?(2)相似比是;(3)△ABC与△A'B'C'周长比为;△ABC与△A'B'C'面积比为.68B'A'ABCC'912323294合作交流合作交流如果△ABC∽△A'B'C',相似比为2,那么△ABC与△A'B'C'的周长比是多少?面积比呢?ABCA'B'C'DD'相似三角形的性质:相似三角形的性质:性质发现性质发现相似三角形的周长比等于相似比,面积比等于相似比的平方.如果△ABC∽△A'B'C',相似比为k,那么你能求出△ABC与△A'B'C'的周长比和面积比吗?如图四边形ABCD∽四边形A'B'C'D',相似比为k(1)四边形ABCD与四边形A'B'C'D'的周长比是多少?ABCDA'B'C'D'(2)四边形ABCD与四边形A'B'C'D'的面积比是多少?''''''''''''DADCCBBAADCDBCABCCDCBAABCD四边行四边形''''''''''DCBDBABCDABDDCBAABCDSSSSSS△△△△四边形四边形=k=k2师生互动师生互动,,典例示范典例示范例2如图所示,将△ABC沿BC方向平移得到△DEF,△ABC与△DEF重叠部分(图中阴影部分)的面积是△ABC的面积的一半,已知BC=2,求△ABC平移的距离.梳理知识,颗粒归仓小结小结1.1.相似三角形的性质:相似三角形的性质:相似三角形的周长比等于相似比,面积比等于相似比的平方.2.2.相似相似nn边形的边形的周长比等于相似比,面积比等于相似比的平方.课本P111:2,3布置作业,强化理解