导数的几何意义VIP免费

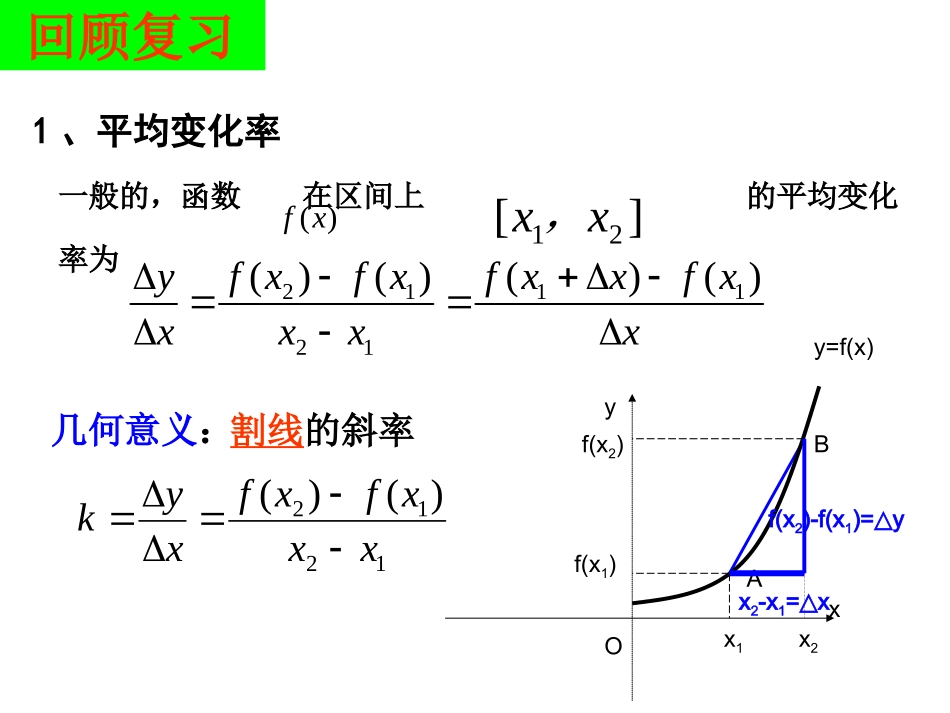
3.1.3导数的几何意义1、平均变化率一般的，函数在区间上的平均变化率为)(xf][21x，x211121()()()()fxfxfxxfxyxxxx几何意义：1212)()(xxxfxfxykOABxyy=f(x)x1x2f(x1)f(x2)x2-x1=x△f(x2)-f(x1)=y△回顾复习割线的斜率2.导数的概念00000()()()limlimxxfxxfxffxxx)(xfy0x3.求函数在处的导数的步骤（1）求平均变化率（2）取极限练习：求函数y=x2+1在x=2处的导数。思考1：在平面中我们是怎样判断一条直线是否是圆的切线？思考2：能否将圆的切线的定义推广为一般曲线的切线定义？与曲线只有一个公共点的直线一定是切线吗？切线与曲线的交点只有一个吗？思考3：如何定义曲线在某一点处的切线？思考4：如何求曲线在某一点处的切线？下面来看导数的几何意义:βy=f(x)PQMΔxΔyOxyβPy=f(x)QMΔxΔyOxy如图,曲线C是函数y=f(x)的图象,P(x0,y0)是曲线C上的任意一点,Q(x0+Δx,y0+Δy)为P邻近一点,PQ为C的割线,yx我们知道是割线PQ的斜率新课探究请看当点Q沿着曲线逐渐向点P接近时,割线PQ的变化趋势是什么？PQoxyy=f(x)割线切线T我们发现,当点Q沿着曲线无限接近点P即Δx→0时,割线PQ趋近于确定的位置PT.我们把直线PT称为曲线在点P处的切线.那么当Δx→0时,割线PQ的斜率就无限趋近于切线PT的斜率。即:'00000()()()limlimxxfxxfxykfxxx切线这个概念:①提供了求曲线上某点切线的斜率的一种方法;②切线斜率的本质——函数在x=x0处的导数.0fxxx因此在处的导数就是切线PT的斜率，即做一做：《优化探究》第3页，题组冲关第2题例1、如图，它表示跳水运动中高度随时间变化的函数h(t)=-4.9t2+6.5t+10的图象。根据图象，请描述、比较曲线h(t)在t0,t1,t2附近的变化情况。htol2l0t4t3t2t0t1l1htol2l0t4t3t2t0t1l1典例分析解：我们用曲线h(t)在t0,t1,t2处的切线，刻画曲线h(t)在上述三个时刻附近的变化情况。(1)当t=t0时,曲线h(t)在t0处的切线l0平行于x轴.所以,在t=t0附近曲线比较平坦,几乎没有下降.(2)当t=t1时,曲线h(t)在t1处的切线l1的斜率h′(t1)<0.所以,在t=t1附近曲线下降,即函数h(t)在t=t1附近单调递减.(3)当t=t2时,曲线h(t)在t2处的切线l2的斜率h′(t2)<0.所以,在t=t2附近曲线下降,即函数h(t)在t=t2附近也单调递减.与t2相比,曲线在t1附近下降得缓慢些.00()()()limlimxxyfxxfxfxyxx在不致发生混淆时，导函数也简称导数．000()()()()().yfxxfxfxfxx函数在点处的导数等于函数的导函数在点处的函数值导函数由函数f(x)在x=x0处求导数的过程可以看到,当x=x0时,f’(x0)是一个确定的数.那么,当x变化时,便是x的一个函数,我们叫它为f(x)的导函数.即:新课探究如：f（x）=x2+1如何求函数y=f(x)的导数?(1)()();yfxxfx求函数的增量(2):()();yfxxfxxx求函数的增量与自变量的增量的比值0(3)()lim.xyyfxx求极限，得导函数（3）函数f(x)在点x0处的导数就是导函数在x=x0处的函数值，即。这也是求函数在点x0处的导数的方法之一。)(0xf)(xf0|)()(0xxxfxf（2）函数的导数，是指某一区间内任意点x而言的,就是函数f(x)的导函数。)(xf（1）函数在一点处的导数，就是在该点的函数的改变量与自变量的改变量之比的极限，它是一个常数，不是变数。1.弄清“函数f(x)在点x0处的导数”、“导函数”、“导数”之间的区别与联系。小结