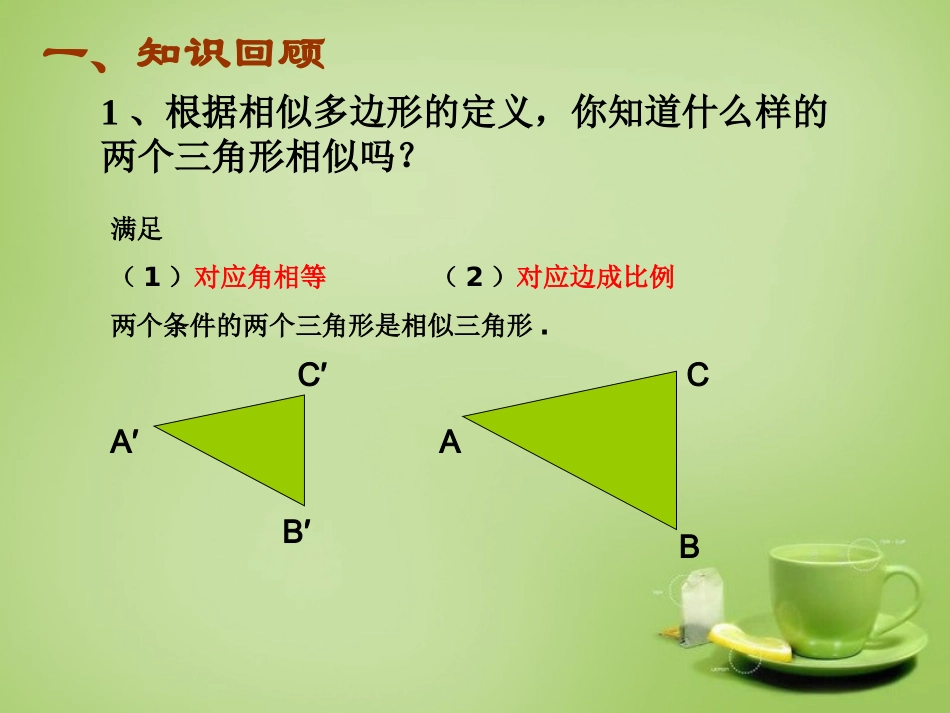
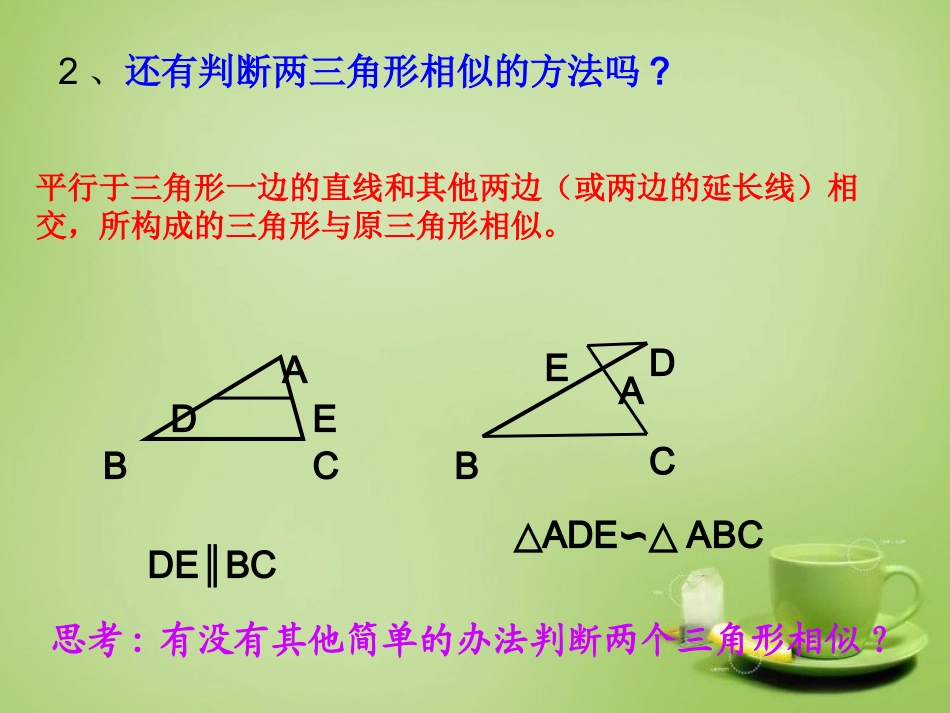
一、知识回顾1、根据相似多边形的定义,你知道什么样的两个三角形相似吗?满足(1)对应角相等(2)对应边成比例两个条件的两个三角形是相似三角形.ABCB′C′A′2、还有判断两三角形相似的方法吗?DEBC∥△ADEABC∽△DEABCABCDE平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似。思考:有没有其他简单的办法判断两个三角形相似?二、探究活动:探究1、已知在△ABC和△A′B′C′中.A=A′∠∠∠B=B′′∠求证:△ABCA′B′C′∽△DEA′B′C′ABC在△ABC的边AB(或延长线)上截取AD=A′B′.过点D作DEBC.∥交AC于点E.则有△ADEABC∽△∵∠ADE=BB=B′∠∠∠∴∠ADE=B′∠又∵∠A=A′AD=A′B′∠∴△ADEA′B′C′≌△(ASA)∴△A′B′C′ABC∽△证明:由上面的数学活动我们可以得到判定三角形相似的定理定理1:如果一个三角形的两个角分别与另一个三角形的两个角对应相等.那么这两个三角形相似.(可简单说成:两个角对应相等的两个三角形相似)例题学习例题1:已知在△ABC和△A′B′C′中,∠C和∠C′都是直角,∠A=A′∠求证:△ABCA′B′C′∽△分析:可以用什么方法证明两三角形相似?例题学习例题2:已知在△ABC中,已知DEBC,DFAB,∥∥求证:△ADEEFC∽△分析(1)可以用什么方法证明△ADEEFC∽△?(2)怎样证∠A=CEF,∠C=AED?∠∠例2.如图,△ABC中,DE∥BC,EF∥AB,试说明△ADE∽△EFC.AEFBCD例题分析证明:∵DE∥BC,EF∥AB(已知),∴∠ADE=∠B=∠EFC(两直线平行,同位角相等)∠AED=∠C.(两直线平行,同位角相等)∴△ADE∽△EFC.(两个角分别对应相等的两个三角形相似.)练习:1、△ABC和△A′B′C′中∠A=80°、∠B=40°、∠A′=80°、∠C′=60°.那么这两个三角形相似吗?2、等边三角形都相似吗?3、有一个内角对应相等的两个等腰三角形相似吗?4、各有一个内角为100°的两个等腰三角形相似吗?1、如图,在ABCD中,E是边BC上的一点,且BE:EC=3:2,连接AE、BD交于点F,则BE:AD=_____,BF:FD=_____。2、如图,在△ABC中,∠C的平分线交AB于D,过点D作DEBC∥交AC于E,若AD:DB=3:2,则EC:BC=______。ABCDEFABCED反馈练习:3:53:53:5反馈练习:3、如图C是线段BD上的一点ABBD.EDBD.ACEC⊥⊥⊥求证:△ABCCDE∽△EA1BCD2证明:∵ABBD⊥、EDBD⊥∴∠ABC=CDE=90°∠∴∠1+A=90°∠∵ACEC⊥∴∠1+2=90°∠∴∠A=2∠∴△ABCCDE∽△4.已知D、E分别是△ABC的边AB,AC上的点,若∠A=35°,C=85°,AED=60°∠∠则AD·AB=AE·ACABCDE相似三角形的识别方法有那些?方法1:通过定义三个角对应相等三边对应成比例总结梳理总结梳理方法2:平行于三角形一边的直线。方法3:两角对应相等,两三角形相似。达标检测•1.(2014•江阴市模拟)下列条件中,能判定两个等腰三角形相似的是()•A.都含有一个30°的内角B.都含有一个45°的内角•C.都含有一个60°的内角D.都含有一个80°的内角C•2.如图,在△ABC中.∠ACB=90°,CDAB⊥于点D,则图中相似三角形共有()•A.1对B.2对C.3对D.4对达标检测C•3.(2014•齐齐哈尔一模)如图,要使△ADBABC∽△,还需增添的条件(写一个即可).达标检测答案:∠C=∠ABD,不唯一。课外作业•见课本第67页练习第1,2题。