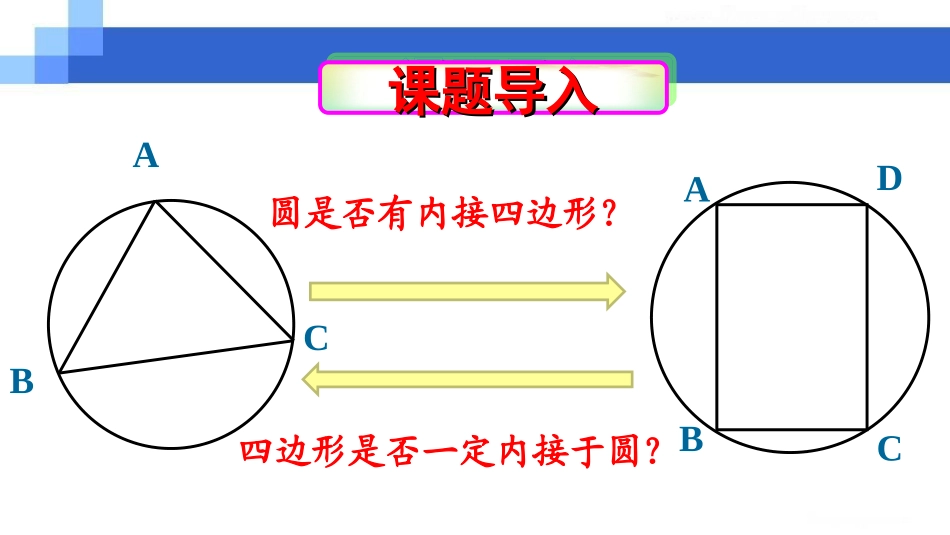
DBAC·O圆内接四边形的性质与判定定理普通高中课程标准实验教科书选修4—1第二讲(二)宁夏银川市第二中学马丽欣课题导入课题导入课题导入课题导入ABCABCD圆是否有内接四边形?四边形是否一定内接于圆?如果多边形的所有顶点都在一个圆上,这个多边形就叫做圆内接多边形,这个圆就是多边形的外接圆.DBAC·O这个多边形有什么特点?探究ABCDABDCABDC观察上图,这组四边形都内接于圆,我们从哪些方面研究圆内接四边形?边的关系角的关系性质判定ADCBOαβOOOOCADBDBOCOA1801803602136021,21,同理可得:则连接定理1圆的内接四边形的对角互补内角定理定理22圆内接四边形的外角等于它的圆内接四边形的外角等于它的内角的对角内角的对角..DEBCDABCEBCABCOO180180而由于ADCBE延长线段AB到点EDEBC外角圆内接四边形的性质:圆内接四边形的性质:定理1圆的内接四边形的对角互补.定理2圆的内接四边形的外角等于它的内角的对角.思考:经过上面的讨论,我们得到了圆内接四边形的两条性质,那么它们的逆命题成立吗?假设:四边形ABCD中,∠B+D=180∠O求证:A、B、C、D在同一圆周上(简称四点共圆)CABDOCABDOE若点D在圆外设E是AD与圆周的交点,连接EC,则有∠AEC+B=180∠0又∠B+D=180∠0可得∠D=AEC.∠这与“三角形的外角大于任一不相邻的内角”矛盾,故点D不可能在圆外。若点D在圆内AD的延长线必与圆相交,设交点为E,连接CE,则∠B+E=180∠0∵∠B+ADC=180∠0∴∠E=ADC∠同样产生矛盾∴点D不可能在圆内综上所述,点D只能在圆周上,即A、B、C、D四点共圆。ABCDEo圆内接四边形判定定理:圆内接四边形判定定理:如果一个四边形的对角互补,那么这个四边形的四个顶点共圆.推论:推论:如果四边形的一个外角等于它的内角的对角,那么这个四边形的四个顶点共圆.例1:如图,⊙O1与⊙O2都经过A、B两点,经过点A的直线CD与⊙O1交于点C与⊙O2交于点D,经过点B的直线EF与⊙O1交于点E与⊙O2交于点F。证明:连接AB∵四边形ABEC是⊙O1的内接四边形∴∠BAD=∠E又∵四边形ADFB是⊙O2的内接四边形∴∠BAD+F=180∠0∴∠E+F=180∠0∴CEDF∥求证:CE∥DF。例2:如图,CF是△ABC的边AB上的高FP⊥BC,FQ⊥AC。求证:A、B、P、Q四点共圆。ABCFPQ证明:连接PQ在四边形QFPC中,∵FPBC⊥,FQAC⊥∴∠FQA=FPC∠又∵CFAB⊥∴Q、F、P、C四点共圆∴∠QFC=QPC∠∴∠QFC与∠QFA互余。∴∠A=QFC∠∴∠A=QPC∠∴A、B、P、Q四点共圆DBAC·O小结:圆内接四边形四点共圆1、如图,AD、BE是△ABC的两条高,求证:∠CED=∠ABCABCEDF2、求证:对角线互相垂直的四边形中,各边中点在同一个圆周上。ABCDA`B`C`D`3、如图:已知四边形ABCD内接于圆,延长AB和DC相交于E,EG平分∠E,且与BC、AD分别交于F、G。求证:∠CFG=∠DGFABCDEFG如果四边形一边上的两个顶点的视角相等,那么四边形的四个顶点共圆作业一作业二预习圆的切线的性质及判定定理www.themegallery.com