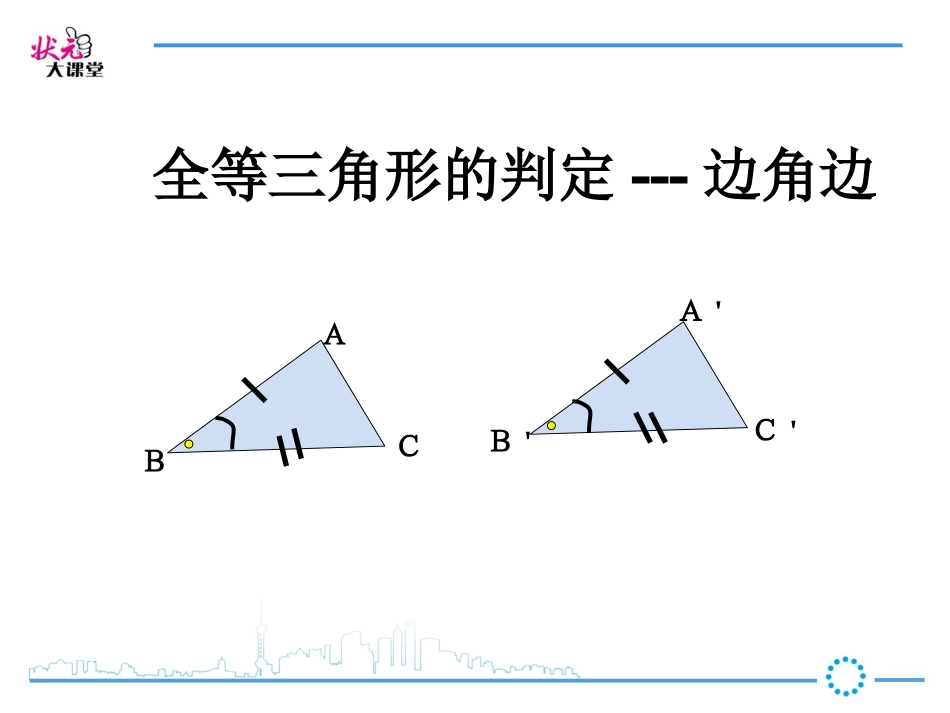
3.边角边边角边ABCA'B'C'新课导入新课导入ABCA'B'C'全等三角形的判定---边角边某厂要制造一批三角形模板,要求是所有的三角形模板必须全等。质检部门为使产品顺利过关,提出了明确的要求:要逐一检查三角形的三条边和三个角是不是都与图纸上的数据一样。但是分别检查三条边和三个角这6个数据非常麻烦.为了提高效率,技术科的“小王”提出是不是可以找到一个更简单的方法,例如只检测一个数据可以吗?或只检测两个数据呢?三个数据呢?推进新课推进新课思考思考如果两个三角形有三组元素(边或角)对应相等,那么会有哪几种可能的情况?有以下的四种情况:(1)两边一角(2)两角一边(3)三角(4)三边思考思考已知两个三角形有两边一角对应相等时,又分为几种情况讨论?思考思考已知两个三角形有两边一角对应相等时,应分为几种情况讨论?边-角-边边-边-角AAA'A'BB'BB'CCC'C'第一种第二种∨∨3cm3cm4cm4cm45°45°AABBCCMM做一做画一个三角形,使它的一个内角等于45°,夹这个角的两条边分别为3厘米和4厘米.步骤:1.画一线段AB,使它等于4cm2.画∠MAB=45°3.在射线AM上截取AC=3cm4.连结BC.△ABC就是所求做的三角形.把你们所画的三角形剪下来与同桌所画的三角形进行比较,它们能完全重合吗?在△ABC和△DEF中,已知AB=DE=3㎝,∠B=E=30∠0,BC=EF=5㎝,它们是否全等?验证结论验证结论3㎝5㎝300DEF3㎝5㎝300ABC用符号语言表达为:在△ABC与△DEF中AB=DE∠B=∠EBC=EF∴△ABC≌△DEF(S.A.S.)ABCDEF如果两个三角形有两边及其夹角分别对应相等,那么这两个三角形全等。简记为“SAS”(或“边角边”)三角形全等识别方法三角形全等识别方法三角形全等识别方法三角形全等识别方法画一个三角形,使一个角为45°这个角的邻边为16cm,对边的长度为12cm.动手画一画,把你们所画的三角形剪下来与同桌所画的三角形进行比较,它们能互相重合吗?你发现了什么?ABC12cm16cm45°12cm结论:两边及其一边所对的角相等,两个三角形不一定全等做一做MB’步骤:1.画一线段AC,使它等于16cm2.画∠CAM=45°3.以C为圆心,12cm长为半径画弧,交AM于点B4.连结CB△ABC就是所求做的三角形显然:△ABC与△AB’C不全等和B’、CB’与△AB’C•(一)如果两个三角形有两边及其夹角分别对应相等,那么这两个三角形全等。•(二)如果两个三角形有两边一角对应相等,那么这两个三角形不一定全等。结论结论如图,在△ABC中,AB=AC,AD平分∠BAC,求证:△ABDACD≌△.证明:∵AD平分∠BAC,∴∠BAD=∠CAD.在△ABD与△ACD中,AB=AC,(已知)∠BAD=∠CAD,(已证)AD=AD,(公共边)∴△ABDACD≌△(S.A.S.)∵典例分析典例分析已知:如图,AB=CB,BD平分∠ABC。问∠A=C∠吗?分析:A=C∠∠△ABD≌△CBD边:角:边:AB=CB(已知)∠ABD=∠CBD(已知)?ABCD↓点M是等腰梯形ABCD底边AB的中点,求证∠ADM=∠BCM.证明:证明:∵点M是AB的中点∴AM=BM∵AD=BC∴∠A=∠B在△ADM和△BCM中AD=BC∠A=∠BAM=BM∴△ADMBC≌△M(S.A.S.)∴∠ADM=∠BCM.(全等三角形的对应角相等)因铺设电线的需要,要在池塘两侧A、B处各埋设一根电线杆(如图),因无法直接量出A、B两点的距离,现有一足够长的米尺。请你设计一种方案,粗略测出A、B两杆之间的距离。AB随堂演练随堂演练小明的方案:在池塘旁取一个能直接到达A和B处的点C,连结AC并延长至D点,使AC=DC,连结BC并延长至E点,使BC=EC,连结ED,用米尺测出DE的长,这个长度就等于A,B两点的距离。请你说明理由。AC=DC∠ACB=DCE∠BC=EC△ACBDCE≌△AB=DEABCCEEDD在△ACB和△DCE中在△ACB和△DCE中1:三角形全等的条件,有两边和它们的夹角对应相等的两个三角形全等。(边角边或S.A.S)2:“边边角”能不能判定两个三角形全等呢?(不能)课后小结课后小结完成练习册本课时对应习题课后作业课后作业必须记住我们学习的时间有限的。时间有限,不只由于人生短促,更由于人事纷繁。——斯宾塞