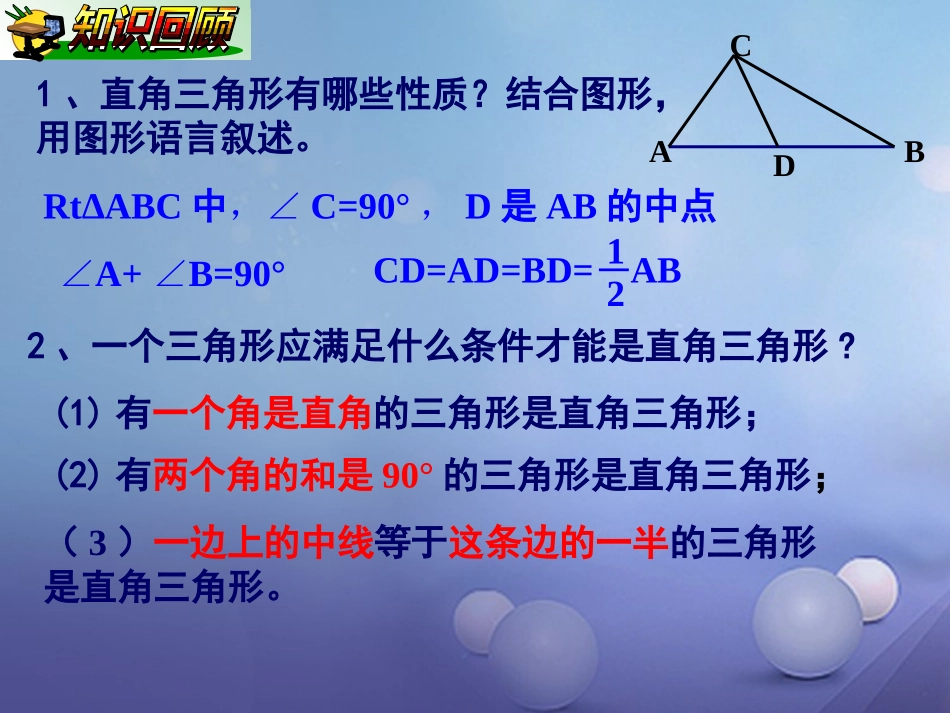
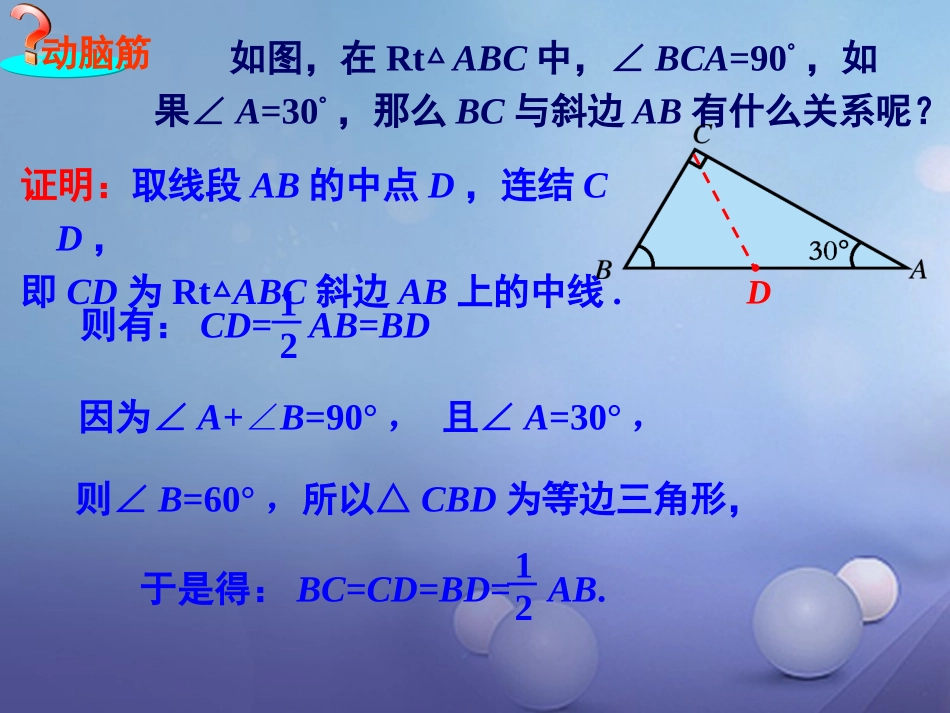
湘教版SHUXUE八年级下本课内容本节内容1.1.21、直角三角形有哪些性质?结合图形,用图形语言叙述。Rt∆ABC中,∠C=90°,D是AB的中点DCBA∠A+B=90°∠CD=AD=BD=AB122、一个三角形应满足什么条件才能是直角三角形?(1)有一个角是直角的三角形是直角三角形;(2)有两个角的和是90°的三角形是直角三角形;(3)一边上的中线等于这条边的一半的三角形是直角三角形。动脑筋如图,在Rt△ABC中,∠BCA=90°,如果∠A=30°,那么BC与斜边AB有什么关系呢?D证明:取线段AB的中点D,连结CD,即CD为Rt△ABC斜边AB上的中线.则有:CD=AB=BD12因为∠A+∠B=90°,且∠A=30°,则∠B=60°,所以△CBD为等边三角形,于是得:BC=CD=BD=AB.12结论在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.直角三角形性质定理:CBA30°图形语言:已知△ABC中,∠ACB=90°,∠B=30°(∠A=60°),那么:AC=AB12还有其他方法证明这个定理吗?还有其他方法证明这个定理吗?DACB300600你能用等边三角形的性质来证明直角三角形的这条性质吗?(1)延长BC到D,使CD=BC,连接AD(2)将△ABC沿AC对折,得到轴对称图形△ADC。这样构成等边△ADB可证得:AB=DC=2BC,即:BC=AB12解:取线段AB的中点D,连结CD,即CD为Rt△ABC斜边上的中线,动脑筋在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于30°.在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于30°.D于是得到:逆定理如图,在Rt△ABC中,如果BC=AB,那么∠A等于多少?12则有:CD=AB=BD12又BC=AB,所以CD=BD=BC,12即:△BDC为等边三角形,于是∠B=60°.而∠A+∠B=90°,所以∠A=30°.举例例1在A岛周围20海里(1海里=1852m)水域内有暗礁,一轮船由西向东航行到O处时,发现A岛在北偏东60°的方向,且与轮船相距海里,如图.该船如果保持航向不变,有触暗礁的危险吗?303北东BD60°303分析:轮船在航行过程中,如果与A岛的距离始终大于20海里,则轮船就不会触暗礁.解:过A点作AD⊥OB,垂足为D.在Rt△AOD中,海里,∠AOD=30°.=303AO所以轮船不会触礁.于是:AD=AO=×3012√312≈25.98(海里)>20海里EDCBA例2、在∆ABC中,∠B=30°,DE是AB的垂直平分线交BC于点D,AD平分∠BAC,已知AB=8cm,求AC长。分析:由∠B=30°,AC就等于AB的一半吗?注意:先要判断∆ABC是直角三角形,再用定理计算。解: DE是AB的垂直平分线∴BD=AD,∠B=∠BAD=30°又 AD平分∠BAC,∴∠BAD=∠CAD=30°,即:∠BAC=2∠BAD=60°∴∠ACB=90°,即:∆ABC是直角三角形. ∠B=30°,AB=8cm∴AC=AB=4cm121、在RtABC△中,∠C=90°,若∠A=30°,且BC=3,则AB的长是。CAB6602、如图:在RtABC△中,∠C=90°,AB=4,BC=2,则∠B=°3、如图所示,一个人从山下A点沿30°的坡路登上山顶,他走了500米后到达山顶的点B,则这座山的高度是米CAB30°2505、如图,在RtABC△中,∠C=90°,∠A=30°,BD是∠B的平分线,AC=18,则BD的值为()A、4.9B、9C、12D、15ABDCCABCDA4、如图在△ABC中,ADBC⊥,∠C=45°,AB=2,DC=,则∠B=()A、30°B、45°C、60°D、75°√3√36、如图所示,在Rt△ABD中,∠D=90°,C为AD上一点,则x可能是().A.40°B.30°C.20°D.10°C此题题目中除了直角并未给出任何其他角的具体度数,因此要求出x值,只能大致估计其范围,再在选项中选择可能的取值. 6x>90,∴x>15.又6x<180,∴x<30.故,应选择C.DCBA6x7、如图所示,在锐角三角形ABC中,CD,BE分别是AB,AC边上的高,且CD,BE交于一点P,若∠A=50°,则∠BPC的度数是().A.150°B.130°C.120°D.100°PEDCBAB BE,CD是AB,BC的高,∴∠BDP=90°,∠BEA=90°.又∠A=50°,∴∠ABE=90°-∠A=90°-50°=40°.∴∠ABE=90°-∠A=90°-50°=40°.故,应选择B.9、如图,是某商店营业大厅电梯示意图.电梯AB的倾斜角为30°,大厅两层之间的距离BC为6米.你能算出电梯AB的长度吗?AB=12米.8、p6练习2∠A=30°.10、下图是屋架设计图的一部分,其中BCAC⊥,DEAC⊥,点D是AB的中点,∠A=30...