定积分yongVIP免费

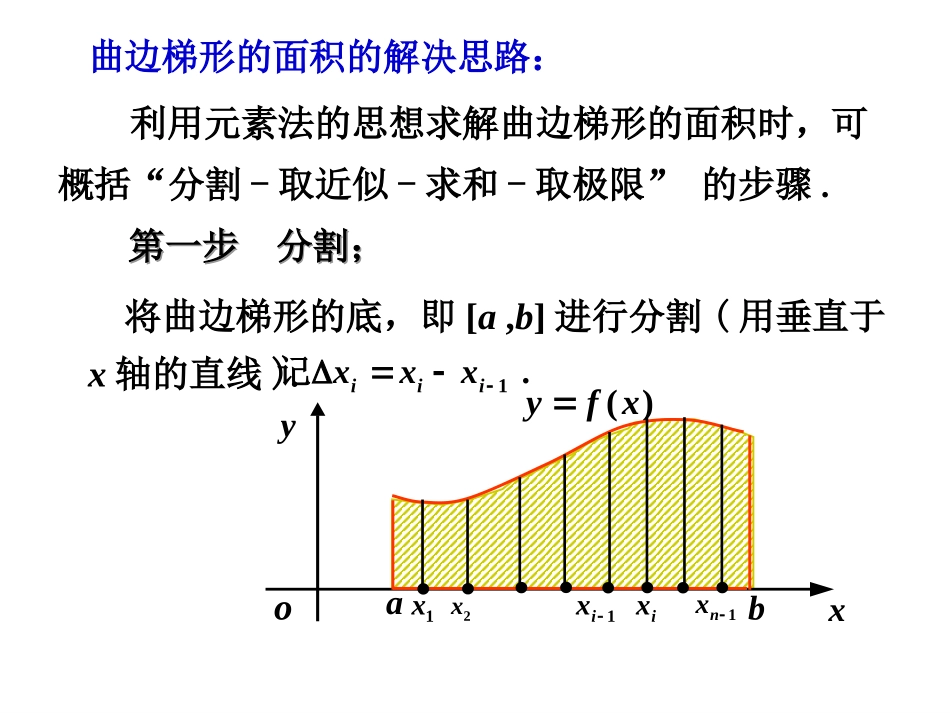
定积分利用元素法的思想求解曲边梯形的面积时，可概括“分割-取近似-求和-取极限”的步骤.将曲边梯形的底，即[a,b]进行分割(用垂直于x轴的直线).第一步分割；第一步分割；曲边梯形的面积的解决思路：abxyo)(xfyix1x1ix1nx2x记1.iiixxx取出典型小区域，用矩形面积近似曲边梯形面积.第二步取近似；第二步取近似；abxyo)(xfy用矩形面积近似用矩形面积近似小曲边梯形面积小曲边梯形面积()if高底ix1x1ix1nx2xix典型小区域面积iSi().iiiSfxabxyo)(xfyix1x1ix1nx2x第三步求和；第三步求和；i矩形面积和与曲边梯形面积不相等有误差有误差121nn11().nniiiiiSfx将每个小曲边梯形的面积都用矩形近似，并将所有的小矩形面积加起来.第四步取极限.第四步取极限.当对曲边梯形底的分割越来越细时，矩形面积之和越近似于曲边梯形面积.abxyo)(xfy0,1,2,,ixinmax{}0ix11()nniiiiiASfx112233()()()(),nnfxfxfxfxiniixfA)(lim101122330lim[()()()()].nnfxfxfxfx曲边梯形面积的近似值为:曲边梯形面积为当即小区间的最大长度趋近于零时分割无限加细12,max{,,,}(0),nxxx2.变速直线运动的路程2.变速直线运动的路程设一物体作直线运动，已知速度v=vt是时间t的连续函数，求在时间间隔[T1,T2]上物体所经过的路程s.(1)分割在时间间隔[T1,T2]内任意插入n1个分点：T1=t0