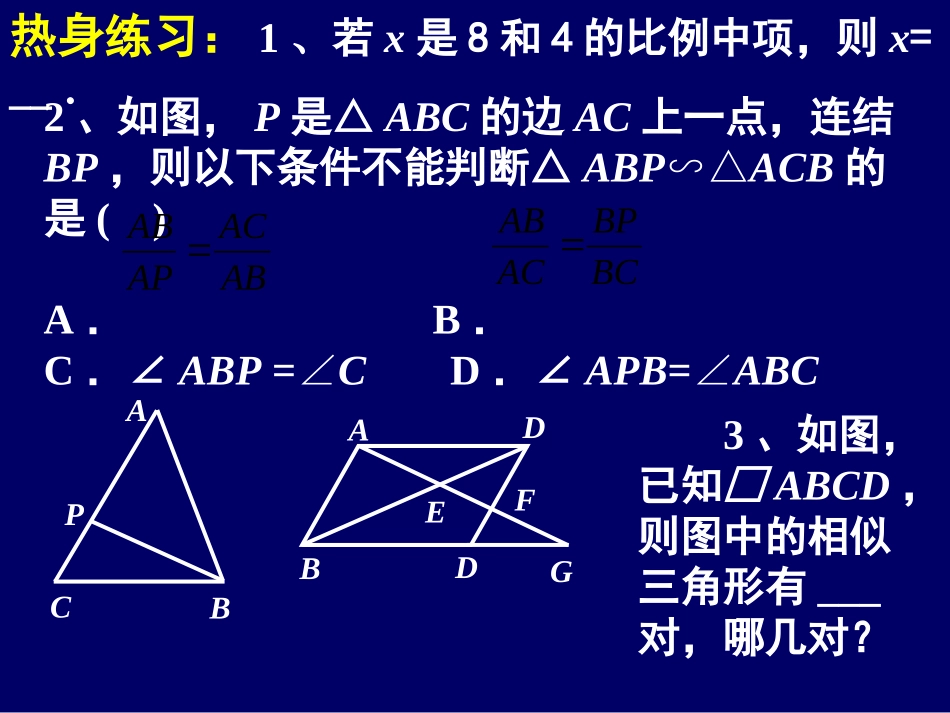
初三第一轮总复习几何第15课时图形的相似【本课知识点】1、掌握相似图形的性质、判定;2、汇灵活运用相似图形的性质解决综合问题.热身练习:1、若x是8和4的比例中项,则x=__.ABCP2、如图,P是△ABC的边AC上一点,连结BP,则以下条件不能判断△ABP∽△ACB的是()A.B.C.∠ABP=∠CD.∠APB=∠ABCABACAPABBCBPACAB3、如图,已知□ABCD,则图中的相似三角形有___对,哪几对?DEABDFG4、如图正方形ABCD中,点E在AB上,且AE:EB=2:1,AF⊥DE于G,交BC于F,则△AEG的面积与四边形BEGF的面积之比是___.FEDCBAG5、如图,在Rt△ABC中(∠C=90°),放置边长分别为3、4、x的三个正方形,则x=___.ABC34x6、如图,点M是△ABC内的一点,过点M分别作直线平行于△ABC各边,所围成的三个小三角形△1,△2,△3(图中阴影部分)的面积分别是4,9和49.则△ABC的面积是_____.7、如图,路灯距地面8米,身高1.6米的小明从距离灯的底部(点O)20米的点A处,沿AO所在直线行走14米到点B时,人的影长度()A.变长3.5米B.变长2.5米C.变短3.5米D.变短2.5米ABC△1M△2△3OBNAM例、如图,在Rt△ABC中,∠C=90°,翻折∠C,使点C落在斜边AB上某一点D处,折痕为EF(点E、F分别在AC、BC上).(1)若△CEF与△ABC相似.①当AC=BC=2时,AD的长为_______;②当AC=3,BC=4时,AD的长为_______.(2)当点D是AB的中点时,△CEF与△ABC相似吗?为什么?EFCBA例2、如图,在△ABC中,AB=AC=5,BC=6,且△ABC≌△DEF,将△DEF与△ABC重合在一起,△ABC不动,△DEF运动,并满足:点E在BC上沿B到C的方向运动,且DE始终经过点A.(1)求证:△ABE∽△ECM;(2)探究:在△DEF运动过程中,重叠部分能否构成等腰三角形?(3)当线段AM最短时,求重叠部分的面积.ABCFED拓展与延伸:能训:P106第9题C1A1B1654小结:【本课知识点】1、相似的基本性质;2、提高解决综合体的能力.作业:1、能训和时代上相关练习2、预习下节课有关内容