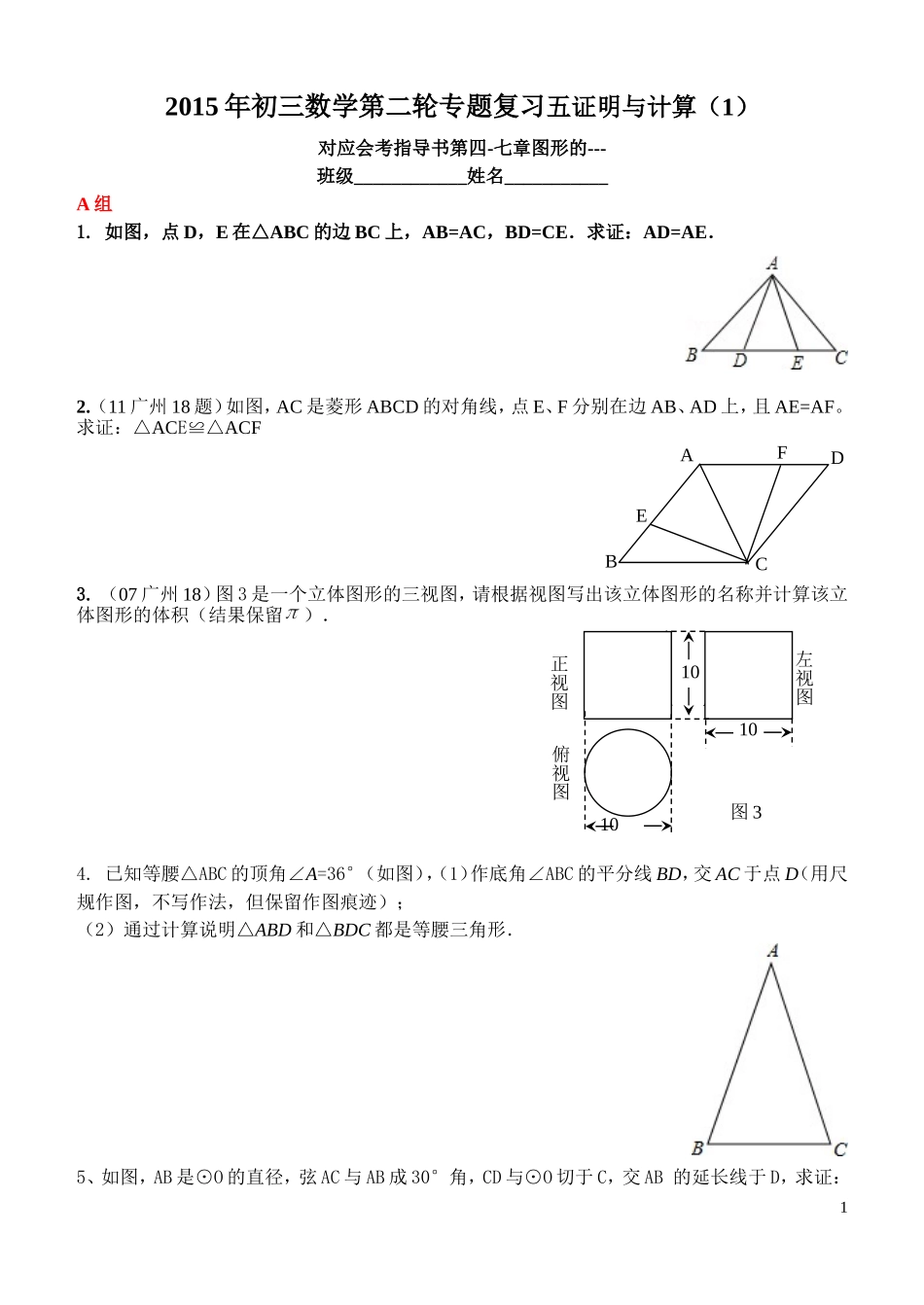
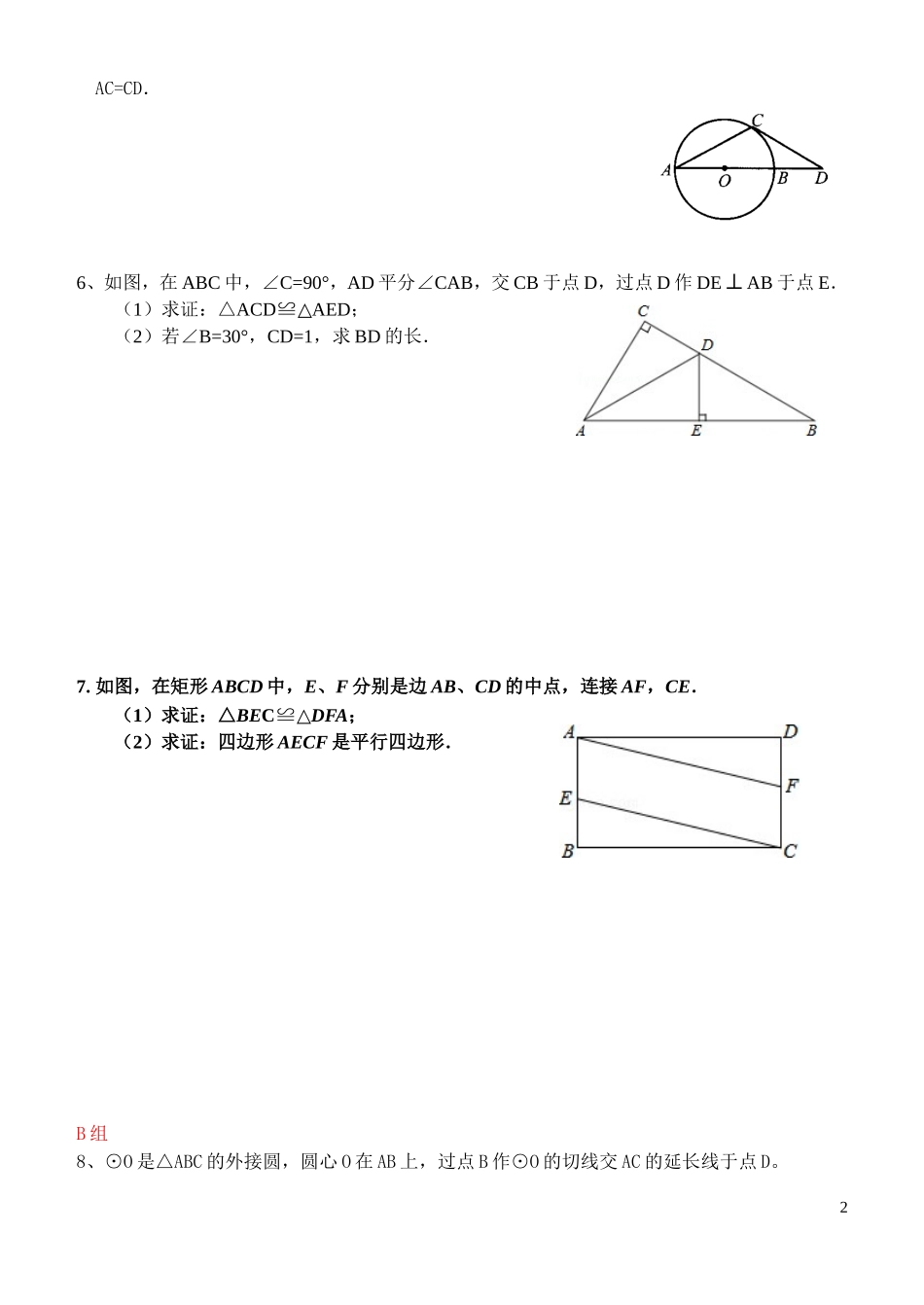
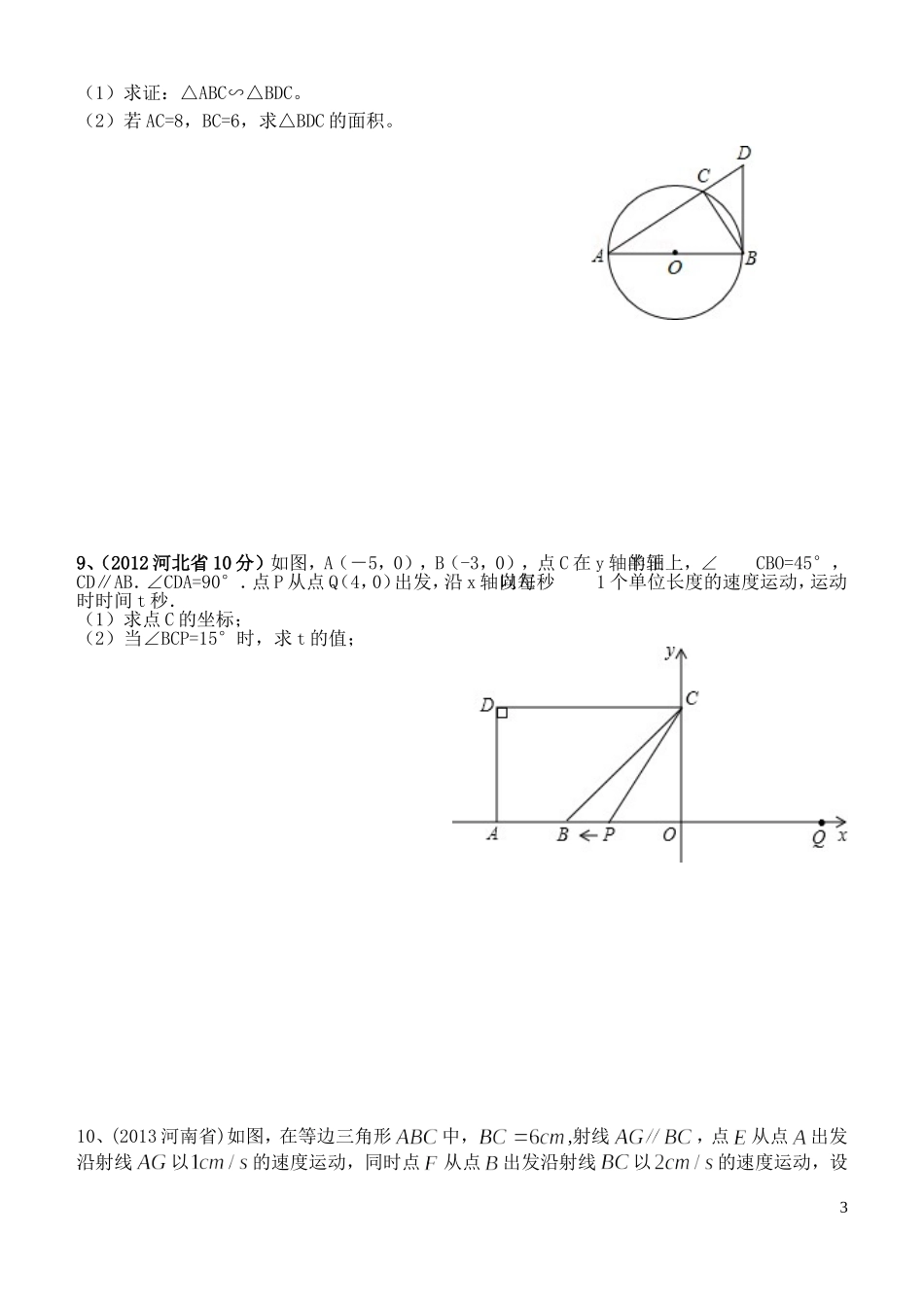
2015年初三数学第二轮专题复习五证明与计算(1)对应会考指导书第四-七章图形的---班级____________姓名___________A组1.如图,点D,E在△ABC的边BC上,AB=AC,BD=CE.求证:AD=AE.2.(11广州18题)如图,AC是菱形ABCD的对角线,点E、F分别在边AB、AD上,且AE=AF。求证:△ACE≌△ACF3.(07广州18)图3是一个立体图形的三视图,请根据视图写出该立体图形的名称并计算该立体图形的体积(结果保留).4.已知等腰△ABC的顶角∠A=36°(如图),(1)作底角∠ABC的平分线BD,交AC于点D(用尺规作图,不写作法,但保留作图痕迹);(2)通过计算说明△ABD和△BDC都是等腰三角形.5、如图,AB是⊙O的直径,弦AC与AB成30°角,CD与⊙O切于C,交AB的延长线于D,求证:1正视图左视图俯视图图3101010ADFEBCAC=CD.6、如图,在ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB于点E.(1)求证:△ACD≌AED△;(2)若∠B=30°,CD=1,求BD的长.7.如图,在矩形ABCD中,E、F分别是边AB、CD的中点,连接AF,CE.(1)求证:△BEC≌△DFA;(2)求证:四边形AECF是平行四边形.B组8、⊙O是△ABC的外接圆,圆心O在AB上,过点B作⊙O的切线交AC的延长线于点D。2(1)求证:△ABC∽△BDC。(2)若AC=8,BC=6,求△BDC的面积。9、(2012河北省10分)如图,A(-5,0),B(-3,0),点C在y轴的正半轴上,∠CBO=45°,CD∥AB.∠CDA=90°.点P从点Q(4,0)出发,沿x轴向左以每秒1个单位长度的速度运动,运动时时间t秒.(1)求点C的坐标;(2)当∠BCP=15°时,求t的值;10、(2013河南省)如图,在等边三角形中,,射线,点从点出发沿射线以的速度运动,同时点从点出发沿射线以的速度运动,设3运动时间为(1)连接,当经过边的中点时,求证:(2)当运动多少s时,四边形是菱形。2015年初三数学第二轮专题复习五证明与计算(2)4PDBCAOCBA对应会考指导书第四-七章图形的---班级____________姓名___________A组1.如图,于点,于点,交于点,且.求证.2.如图所示,已知在平行四边形ABCD中,BE=DF.求证:AE=CF.[来源:学科网]3.如图,.求证:∽.4、如图,已知△ABC内接于⊙O,∠A=45°,BC=2,求⊙O的面积。5.如图,在△ABC中,AB=AC,∠B=60°,∠FAC、∠ECA是△ABC的两个外角,AD平分∠FAC,CD平分∠ECA.求证:四边形ABCD是菱形.5EDCBA6.如图,△ABC是直角三角形,∠ACB=900,利用直尺和圆规按下列要求作图,并在图中表明相应的字母。(保留痕迹,不写作法)作BAC的平分线,交BC于点O;以O为圆心,OC为半径作圆。综合运用:在你所作的图中,(1)AB与⊙O的位置关系是;(直接写出答案)(2)若AC=5,BC=12,求⊙O的半径。7、(2013凉山州)如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(10,0),(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,求点P的坐标.B组8.如图,AB∥,,分别是与的角平分线,点E在AD上。求证:69.(2014·云南昆明)如图,将边长为6cm的正方形ABCD折叠,使点D落在AB边的中点E处,折痕为FH,点C落在Q处,EQ与BC交于点G,求△EBG的周长。C组10、(2014•广西来宾)如图,AB为⊙O的直径,BF切⊙O于点B,AF交⊙O于点D,点C在DF上,BC交⊙O于点E,且∠BAF=2CBF∠,CGBF⊥于点G,连接AE.(1)直接写出AE与BC的位置关系;7QHGFEDCBA(2)求证:△BCG∽ACE△;(3)若∠F=60°,GF=1,求⊙O的半径长.2015年初三数学第二轮专题复习五证明与计算(3)对应会考指导书第四-七章图形的---班级____________姓名___________8PDCBAA组1.(12广州18题)如图6,点D在AB上,点E在AC上,AB=AC,∠B=∠C.求证:BE=CDEDCBA2:如图:点是线段上的一点,.求证:∽3.(11广州20题)5个棱长为1的正方体组成如图的几何体。(1)该几何体的体积是_________(立方单位)表面积是_________(平方单位)(2)画出该几何体的主视图和左视图。4、如图,在△ABC中,AC=BC,点D、E分别是边AB、AC的中点,将△ADE绕点E旋转180°得△CFE,求证:四边形ADCF是矩形5、(07广州21题)如图5,在△ABC中,AB=AC,内切圆O与边BC、AC、AB分别切于点D、E、F.(1)求证:BF=CE;...