《结构力学》_龙驭球_第10章_动力学(3)-12.04修改VIP免费

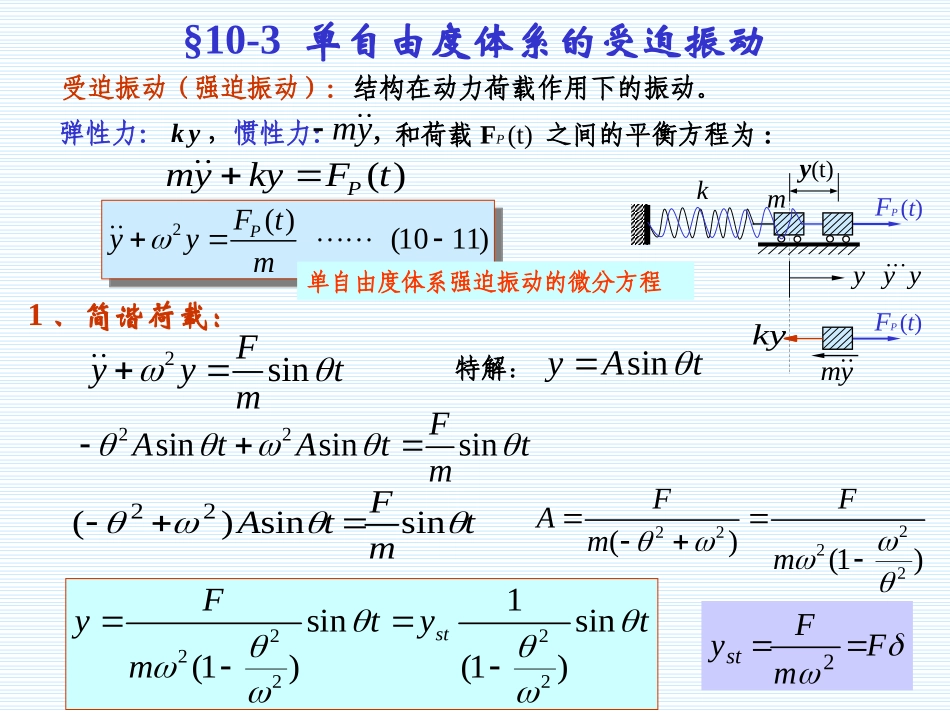
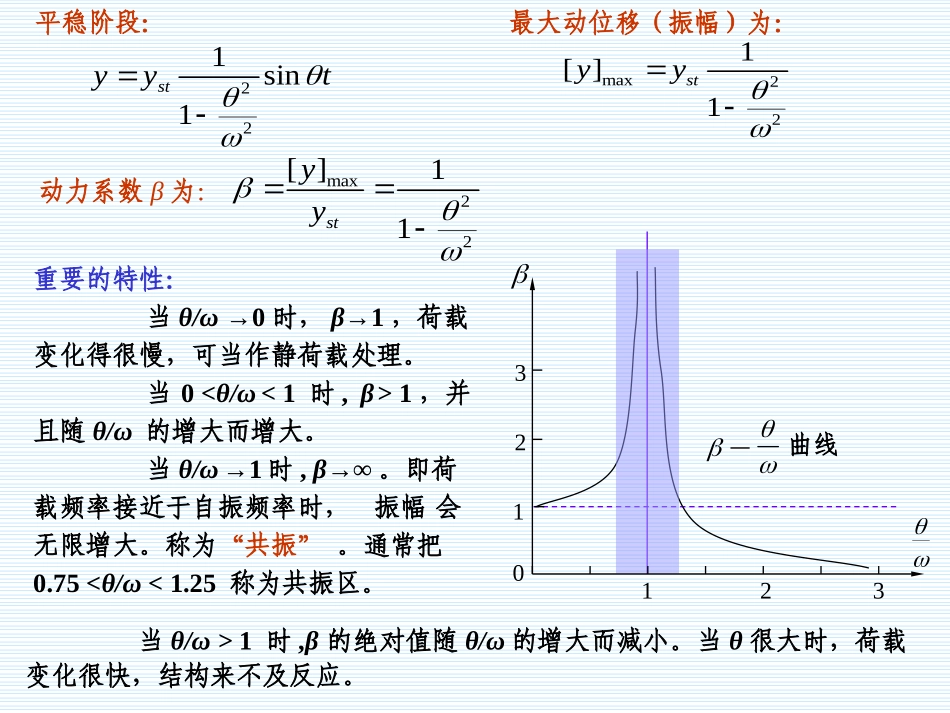
§10-3单自由度体系的受迫振动受迫振动（强迫振动）：结构在动力荷载作用下的振动。kFP(t)弹性力：ky，惯性力：,my和荷载FP(t)之间的平衡方程为:()PmykyFt2()(1011)PFtyym2()(1011)PFtyym1、简谐荷载：y(t)yyymykymFP(t)tmFtAsinsin)(2222222()(1)FFAmmFmFyst2特解：222221sinsin(1)(1)stFytytm2sinFyytmsinyAt22sinsinsinFAtAttm单自由度体系强迫振动的微分方程最大静位移yst：是把动荷载幅值当作静荷载作用时结构所产生的位移。221sin1styyt特解可写为：通解可写为：12221sincossin1styCtCtyt设t=0时的初始位移和初始速度均为零，则：1222,01stCyC221(sinsin)1styytt过渡阶段：振动开始两种振动同时存在的阶段；平稳阶段：后来只按荷载频率振动的阶段。（由于阻尼的存在）按自振频率振动按荷载频率振动平稳阶段：221sin1styyt最大动位移（振幅）为：max221[]1styymax22[]11styy动力系数β为：重要的特性：当θ/ω→0时，β→1，荷载变化得很慢，可当作静荷载处理。当0<θ/ω<1时,β>1，并且随θ/ω的增大而增大。当θ/ω→1时,β→∞。即荷载频率接近于自振频率时，振幅会无限增大。称为“共振”。通常把0.75<θ/ω<1.25称为共振区。当θ/ω>1时,β的绝对值随θ/ω的增大而减小。当θ很大时，荷载变化很快，结构来不及反应。曲线1023123美国的Tacoma(塔克玛)老桥坍塌该桥于1940年11月7日因风力引起的振动而产生断裂当动荷载作用在单自由度体系的质点上时，由于体系上各截面的内力、位移都与质点处的位移成正比，故各截面的最大动内力和最大动位移可采用统一的动力系数，只需将干扰力幅值乘以动力系数按静力方法来计算即可。例：一简支梁（I28b），惯性矩I=7480cm4，截面系数W=534cm3，E=2.1kN/cm2。在跨度中点有电动机重量Q=35kN，转速n=500r/min。由于具有偏心，转动时产生离心力P=10kN，P的竖向分量为Psinθt。忽略梁的质量，试求强迫振动的动力系数和最大挠度和最大正应力。（梁长l=4m）解：⑴求自振频率和荷载频率410SQlEIg13434.57400359807480101.24848Sn13.526050014.32602⑵求动力系数β88.54.573.521111222233max0.804848ststQlPlycmEIEIWlPQWPlWQl4)(44maxstg175.6MPaI22b3570357039.739.71.35对于本例，采用较小的截面的梁既可避免共振，又能获得较好的经济效益。对于本例，采用较小的截面的梁既可避免共振，又能获得较好的经济效益。325149.2⑶求最大正应力0.82必须特别注意，这种处理方法只适用于单自由度体系在质点上受干扰力作用的情况。对于干扰力不作用于质点的单自由度体系，以及多自由度体系，均不能采用这一方法。设体系在t=0时静止，然后有瞬时冲量S作用。2、一般动力荷载一般动荷载作用下的动力反应可利用瞬时冲量的动力反应来推导。瞬时冲量的动力反应：FP(t)tFP瞬时冲量S引起的振动可视为由初始条件引起的自由振动。由动量定理：0PFtSvmm00yΔttmStysin)(Δtτtt-τ()sin()Syttm00PvmSFt如果体系在t=τ时作用瞬时冲量S，则在以后任一时刻t(t＞τ)的位移为()cossinvytytt2()(1011)PFtyym2()(1011)PFtyym单自由度体系强迫振动的微分方程任意荷载FP(t)的动力反应FP(t)tτ()PdSFd整个加载过程可看作由一系列瞬时冲量所组成。例如：在时刻t=τ作用的荷载FP(t)，此时荷载在微分时段dτ内产生的微分冲量为dS。此微分冲量引起如下的动力反应：对于t>τ()sin()PFddytm式(10-15)称为Duhamel积分；这就是初始静止状态的单自由度体系在任意动力荷载作用下的位移公式。01()()sin()(1015)tPytFtdm初始位移y0和初始速度v0不为...