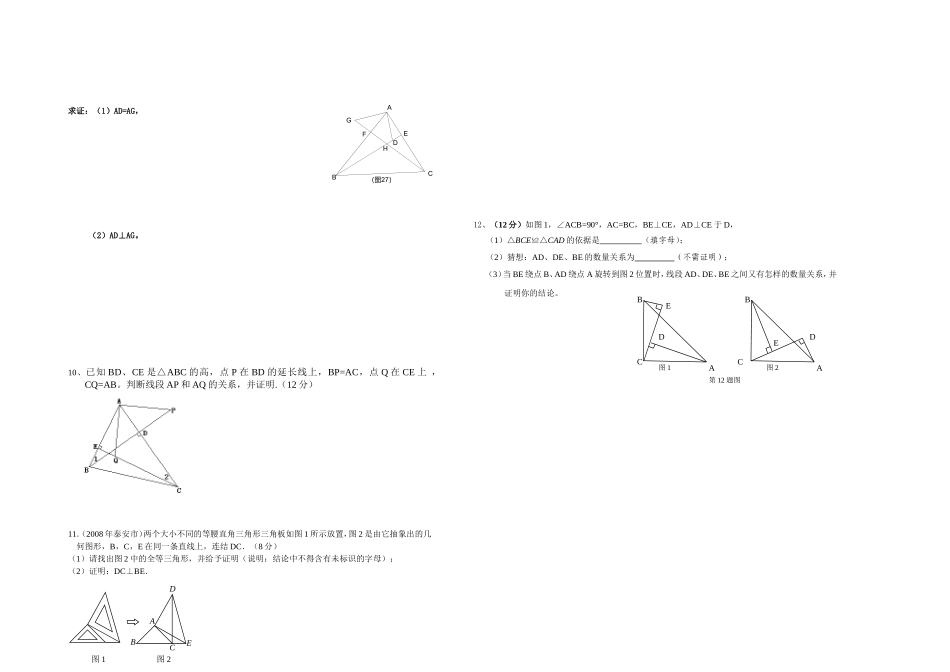
三角形全等的判定专题训练题1.、如图(6):CG=CF,BC=DC,AB=ED,点A、B、C、D、E在同一直线上。求证:(1)AF=EG,(2)BF∥DG。2、如图(12)AB∥CD,OA=OD,点F、D、O、A、E在同一直线上,AE=DF。求证:EB∥CF。3、如图(16)AD∥BC,AD=BC,AE=CF。求证:(1)DE=BF,(2)AB∥CD。4、如图:AB=CD,AE=DF,CE=FB。求证:AF=DE。5、如图:AD=BC,DE⊥AC于E,BF⊥AC于F,DE=BF。求证:(1)AF=CE,(2)AB∥CD。6、如图(10)∠BAC=∠DAE,∠ABD=∠ACE,BD=CE。求证:AB=AC。7.、如图(14)在△ABC中,∠ACB=90°,AC=BC,AE是BC的中线,过点C作CF⊥AE于F,过B作BD⊥CB交CF的延长线于点D。(1)求证:AE=CD,(2)若BD=5㎝,求AC的长。8、如图15△ABC中,AB=2AC,∠BAC=90°,延长BA到D,使AD=AB,延长AC到E,使CE=AC。求证:△ABC≌△AED。9、如图:在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连结AD、AG。GFE(图6)DCBAOFE(图12)DCBAF(图16)EDCBAF(图22)EDCBAF(图24)EDCBAE(图10)DCBAFE(图14)DCBA(图15)EDCBA图1图2DCEAB求证:(1)AD=AG,(2)AD⊥AG。10、已知BD、CE是△ABC的高,点P在BD的延长线上,BP=AC,点Q在CE上,CQ=AB。判断线段AP和AQ的关系,并证明.(12分)11.(2008年泰安市)两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连结DC.(8分)(1)请找出图2中的全等三角形,并给予证明(说明:结论中不得含有未标识的字母);(2)证明:DC⊥BE.12、(12分)如图1,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE于D,(1)△BCE≌△CAD的依据是(填字母);(2)猜想:AD、DE、BE的数量关系为(不需证明);(3)当BE绕点B、AD绕点A旋转到图2位置时,线段AD、DE、BE之间又有怎样的数量关系,并证明你的结论。EBDA图2CBECDA图1第12题图GHF(图27)EDCBA