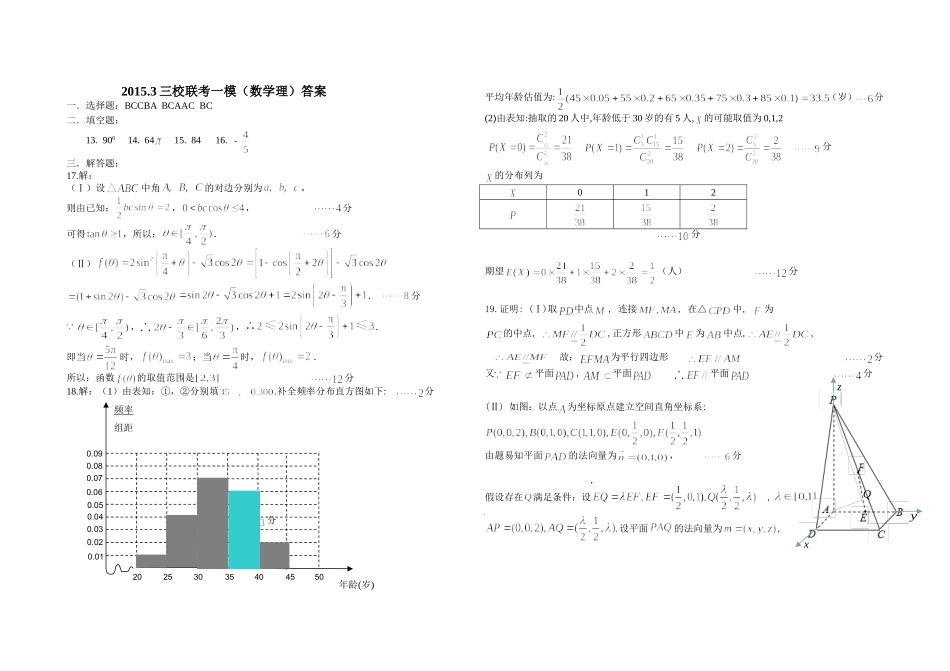
2015.3三校联考一模(数学理)答案一.选择题:BCCBABCAACBC二.填空题:13.90014.6415.8416.三.解答题:17.解:(Ⅰ)设中角的对边分别为,则由已知:,,分可得,所以:.分(Ⅱ).分,,.即当时,;当时,.所以:函数的取值范围是分18.解:(1)由表知:①,②分别填.补全频率分布直方图如下:分分平均年龄估值为:(岁)分(2)由表知:抽取的20人中,年龄低于30岁的有5人,的可能取值为0,1,2分的分布列为012分期望(人)分19.证明:(Ⅰ)取中点,连接,在△中,为的中点,,正方形中为中点,,故:为平行四边形分又平面,平面平面分(Ⅱ)如图:以点为坐标原点建立空间直角坐标系:由题易知平面的法向量为,分假设存在满足条件:设,设平面的法向量为,年龄(岁)0.010.020.030.040.050.060.070.080.0920253035404550频率组距xyzQ分由已知:解得:所以:满足条件的存在,是中点。分20.(1)有已知:,故椭圆方程为分(2)当斜率不存在时:分当斜率存在时:设其方程为:由得由已知:即:分到直线的距离:分此时综上所求:当斜率不存在或斜率为零时:面积取最大值为分21.解(1)由已知:,切点分切线方程:,把代入得:分(2)(Ⅰ)依题意:有两个不等实根设则:①当时:,所以是增函数,不符合题意;分②当时:由得:列表如下:0↗极大值↘依题意:,解得:综上所求:得证;分(Ⅱ)由(Ⅰ)知:变化如下:0+0↘↗↘由表可知:在上为增函数,所以:分又,故由(Ⅰ)知:,设,则成立,所以单调递减,故:,也就是综上所证:成立.分22.选修4-1:几何证明选讲证明:(Ⅰ)连结.∵点是的中点,点是的中点,∴,∴.∵,∴,∴.分在和中,∵,,,∴≌,∴,即.∵是圆上一点,∴是圆的切线.分(Ⅱ)延长交圆于点.∵≌,∴.∵点是的中点,∴.∵是圆的切线,∴.∴.分∵,∴.∵是圆的切线,是圆的割线,∴,∴分23.选修4-4:坐标系与参数方程解:(Ⅰ)由,得:,∴,即,∴曲线的直角坐标方程为.分FCDMOBEA由,得,即,∴直线的普通方程为.分(Ⅱ)将代入,得:,整理得:,由,即,解得:.设是上述方程的两实根,则,分又直线过点,由上式及的几何意义得,解得:或,都符合,因此实数的值为或或.分24.选修4-5:不等式选讲解:(Ⅰ)当时,,,即,解得,又,∴;当时,,,即,解得,又,∴;当时,,,即,解得,又,∴.分综上,不等式的解集为.分(Ⅱ),∴.分∵,使得,∴,整理得:,解得:,因此的取值范围是.分