解直角三角形应用（二VIP免费

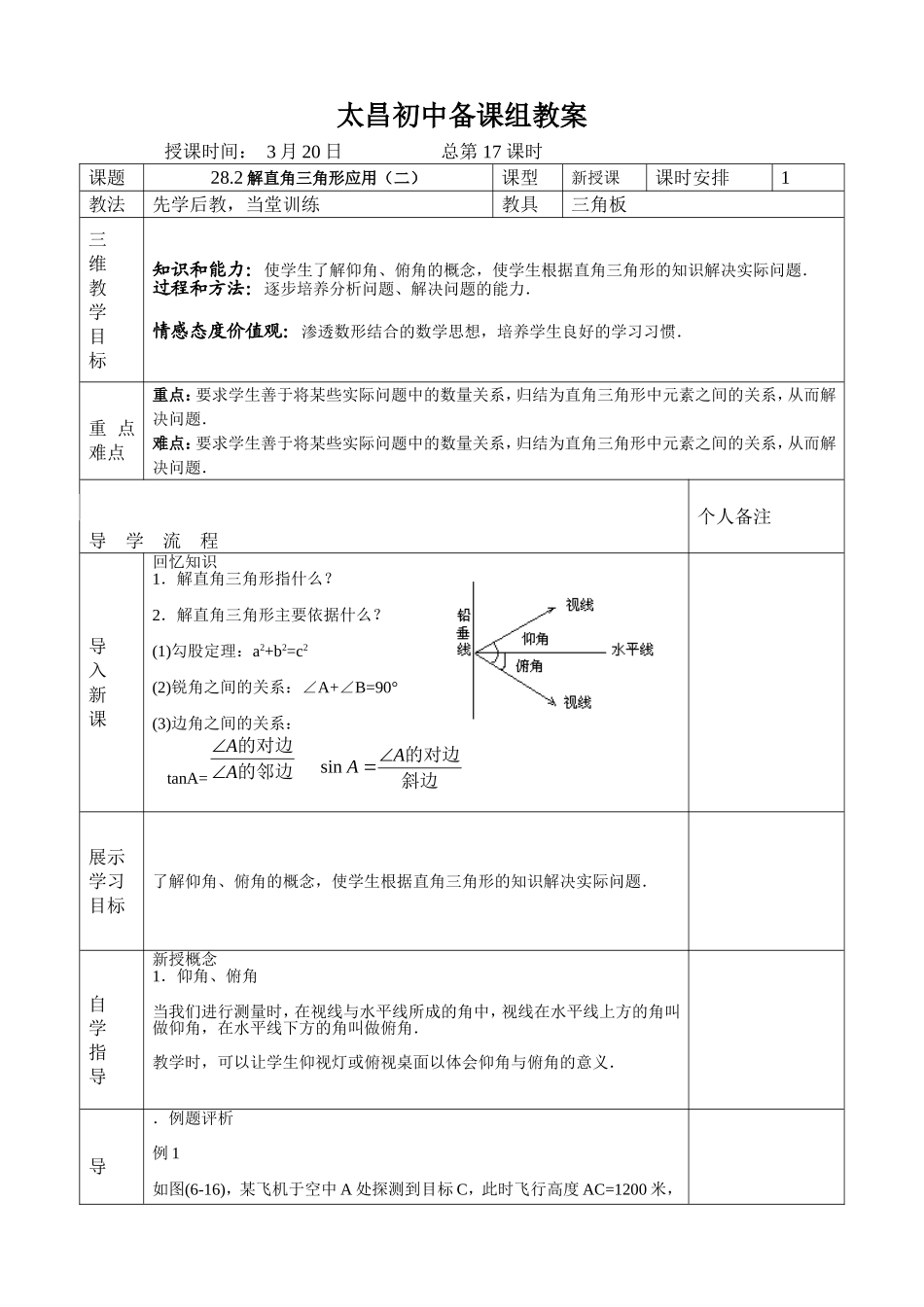
太昌初中备课组教案授课时间：3月20日总第17课时课题28.2解直角三角形应用（二）课型新授课课时安排1教法先学后教，当堂训练教具三角板三维教学目标知识和能力：使学生了解仰角、俯角的概念，使学生根据直角三角形的知识解决实际问题．过程和方法：逐步培养分析问题、解决问题的能力．情感态度价值观：渗透数形结合的数学思想，培养学生良好的学习习惯．重点难点重点：要求学生善于将某些实际问题中的数量关系，归结为直角三角形中元素之间的关系，从而解决问题．难点：要求学生善于将某些实际问题中的数量关系，归结为直角三角形中元素之间的关系，从而解决问题．导学流程个人备注导入新课回忆知识1．解直角三角形指什么？2．解直角三角形主要依据什么？(1)勾股定理：a2+b2=c2(2)锐角之间的关系：∠A+∠B=90°(3)边角之间的关系：tanA=的邻边的对边AA展示学习目标了解仰角、俯角的概念，使学生根据直角三角形的知识解决实际问题．自学指导新授概念1．仰角、俯角当我们进行测量时，在视线与水平线所成的角中，视线在水平线上方的角叫做仰角，在水平线下方的角叫做俯角．教学时，可以让学生仰视灯或俯视桌面以体会仰角与俯角的意义．导．例题评析例1如图(6-16)，某飞机于空中A处探测到目标C，此时飞行高度AC=1200米，斜边的对边AAsin学达标从飞机上看地平面控制点B的俯角α=16°31′，求飞机A到控制点B距离(精确到1米)解：在Rt△ABC中sinB=ABACAB=BACsin=2843.01200=4221(米)答：飞机A到控制点B的距离约为4221米．例1小结：本章引言中的例子和例1正好属于应用同一关系式sinA=斜边的对边A来解决的两个实际问题即已知和斜边，求∠α的对边；以及已知∠α和对边，求斜边．训练提升1．热气球的探测器显示，从热气球看一栋高楼顶部的仰角为，看这栋楼底部的俯角为60，热气球与高楼的水平距离为120m，这栋高楼有多高（结果精确到0.1`m）2．如图6-17，某海岛上的观察所A发现海上某船只B并测得其俯角α=80°14′．已知观察所A的标高(当水位为0m时的高度)为43.74m，当时水位为+2.63m，求观察所A到船只B的水平距离BC(精确到1m)板书设计布置作业教科书P92：3、4后记