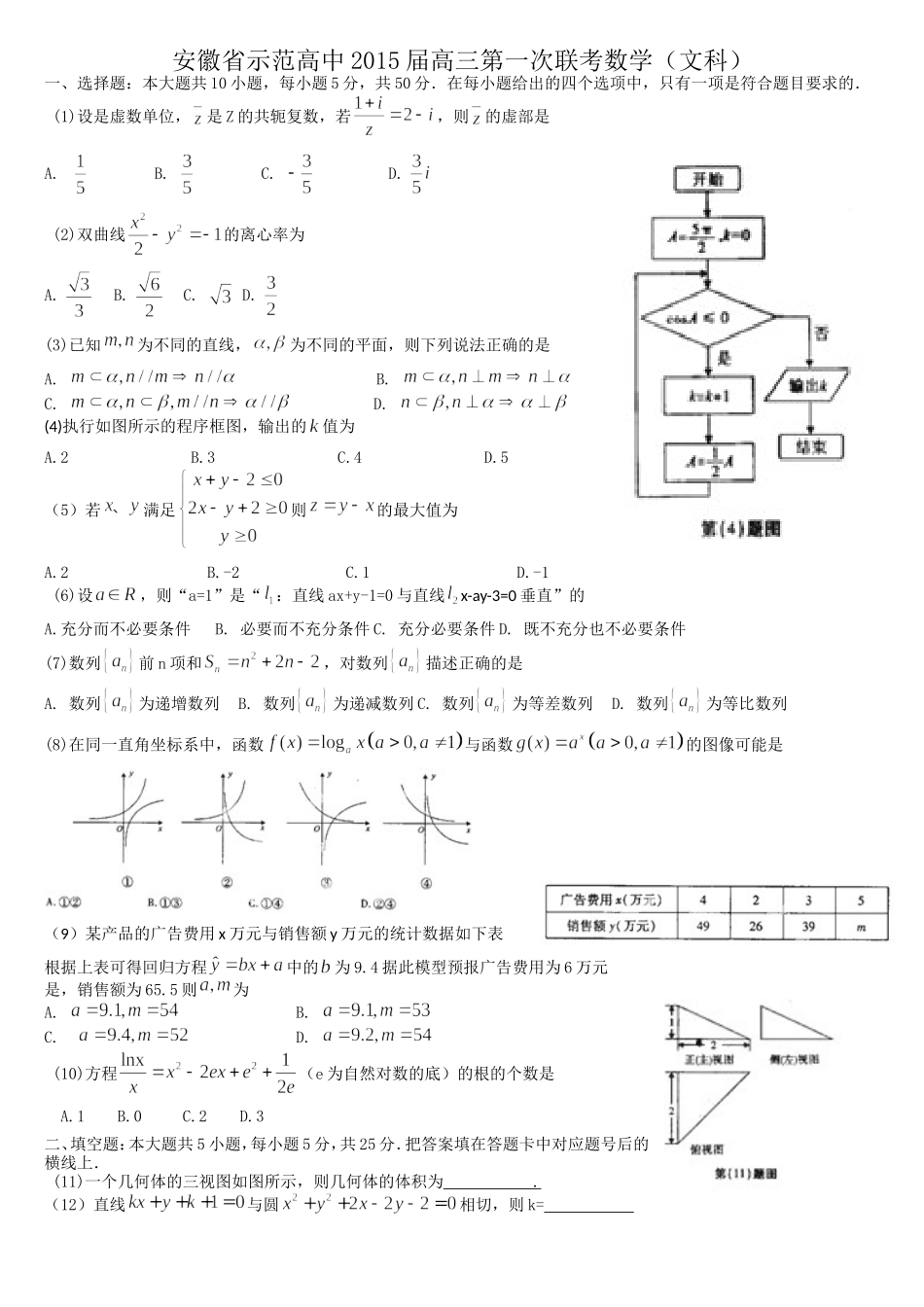
安徽省示范高中2015届高三第一次联考数学(文科)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.(1)设是虚数单位,是Z的共轭复数,若,则的虚部是A.B.C.D.(2)双曲线的离心率为A.B.C.D.(3)已知为不同的直线,为不同的平面,则下列说法正确的是A.B.C.D.(4)执行如图所示的程序框图,输出的值为A.2B.3C.4D.5(5)若满足则的最大值为A.2B.-2C.1D.-1(6)设,则“a=1”是“:直线ax+y-1=0与直线x-ay-3=0垂直”的A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件(7)数列前n项和,对数列描述正确的是A.数列为递增数列B.数列为递减数列C.数列为等差数列D.数列为等比数列(8)在同一直角坐标系中,函数与函数的图像可能是(9)某产品的广告费用x万元与销售额y万元的统计数据如下表根据上表可得回归方程中的为9.4据此模型预报广告费用为6万元是,销售额为65.5则为A.B.C.D.(10)方程(e为自然对数的底)的根的个数是A.1B.0C.2D.3二、填空题:本大题共5小题,每小题5分,共25分.把答案填在答题卡中对应题号后的横线上.(11)一个几何体的三视图如图所示,则几何体的体积为.(12)直线与圆相切,则k=(13)已知函数,则f(f(2))=(14)设,向量,,若,则=(15)已知集合M=|(x,y)|y=f(x)|,若对任意P1(x1,y1)∈M,均不存在P2(x2,y2)∈M,使得x1x2+y1y2=0成立,则称集合M为“好集合”,给出下列五个集合:①M={(x,y)|y=};②M={(x,y)|y=lnx};③M={(x,y)|y=x2+1};④M={(x,y)|(x-2)2+y2=1};⑤M={(x,y)|x2-2y2=1}.其中所有“好集合”的序号是.(写出所有正确答案的序号)三、解答题:本大题共6个小题,共75分.解答应写出文字说明、证明过程或演算步骤.(16)(本小题满分12分)某学校共有30至50岁之间的(包括30与不包括50)数学教师15人,其年龄分布茎叶图如图所示,从中选取3人参加支教.(Ⅰ)若教师年龄分布的极差为15,求教师的平均年龄;(Ⅱ)若选出的3人中有2名男教师1名女教师,将他们分配到两所学校,每校至少有一人,则2名男教师分在同一所学校的概率为多少?(17)(本小题满分12分)已知三角形ABC中,角A,B,C所对的边为a,b,c,2acosA=bcosC+ccosB.(Ⅰ)求A;(Ⅱ)若,求c.(18)(本小题满分12分)直角三角形ABC中,ACB=900,AB=2BC=2,D,E分别为AC,AB的中点,将△ADE沿DF折起,使△ADE沿DE折起,使△ADC为等边三角形,如图所示.(Ⅰ)求证:面ADC⊥面ABC;(Ⅱ)求四棱锥A-BCDE的体积.(19)(本小题满分13分)已知函数(a为常数且a>1,e为自然对数的底),试讨论f(x)的单调性.(20)(本小题满分13分)数列{an}是公比为的等比数列,且1-a2是a1与1+a3的等比中项,前n项和为Sn;数列{bn}是等差数列,b1=8,其前n项和Tn满足Tn=nλ•bn+1(λ为常数,且λ≠1).(Ⅰ)求数列{an}的通项公式及λ的值;(Ⅱ)比较与Sn的大小.(21)(本小题满分13分)设抛物线x2=2py(p>0)的焦点F,过焦点F作y轴的垂线,交抛物线于A、B两点,点M(0,),Q为抛物线上异于A、B的任意一点,经过点Q作抛物线的切线,记为l,l与MA、MB分别交于D、E.(Ⅰ)求证:直线MA、MB与抛物线相切;(Ⅱ)求证安徽省示范高中2015届高三第一次联考数学(文科)1、C解析:设由可得:,解得,所以,则的虚部是,故选C.2、C解析:由转化成标准形式为,易知,所以故选C.3、D解析:A选项可能有,B选项也可能有,C选项两平面可能相交,故选D.4、B解析:k=0时,;k=1时,;k=2时,;k=3时,;故选B.5、A解析:线性可行域如图所示,三个顶点坐标分别为(0,2),(2,0),(-1,0),通过上顶点时Z值最大。故选A.6、A解析:当l1⊥l2,时a-a=0恒成立,故选即a∈R当a=1时l1⊥l2,故选:A7、A解析:⇒,12naaa所以是递增数列;12332321,5,7aaaaaaa不是等差数列3212aaaa也不是等比数列.故选A.8、C解析:当a>1时,利用指数函数与对数函数的单调性可得:①符合;当0<a<1时,同理可得为④.故选:C.9、A解析:ybxa过点6,65.5得9.1a,9.49.1yx因直线过均值点所以7,422xy,...