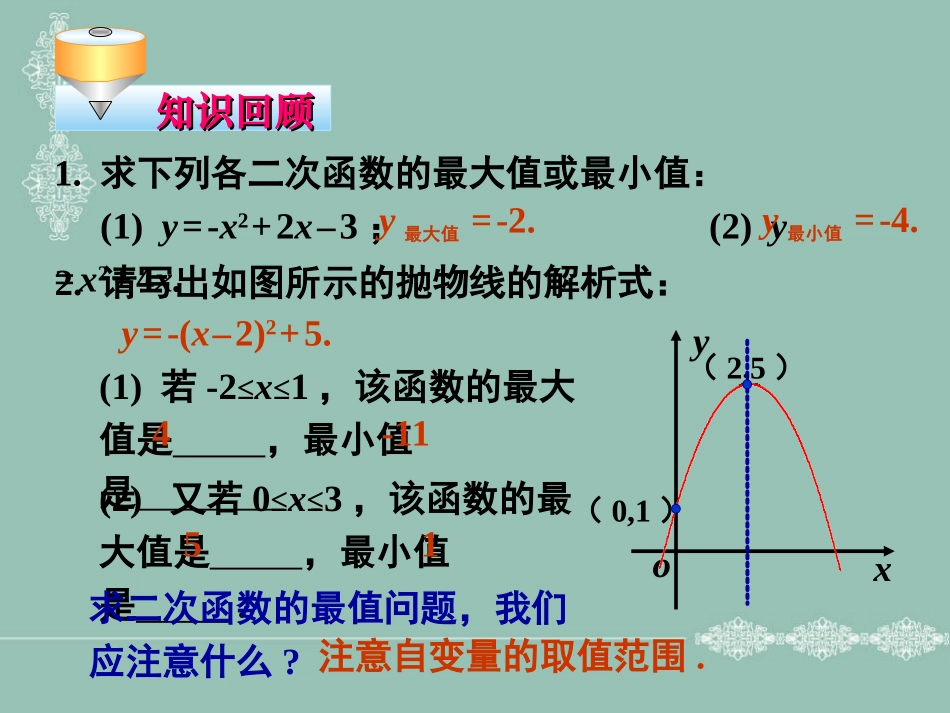
课首课首第第11章二次函数章二次函数1.1.55二次函数的应用二次函数的应用义务教育教科书湘教版九年级数学下册知识回顾知识回顾(0,1)(2,5)xyo2.请写出如图所示的抛物线的解析式:1.求下列各二次函数的最大值或最小值:(1)y=-x2+2x–3;(2)y=x2+4x.(1)若-2≤x≤1,该函数的最大值是,最小值是.(2)又若0≤x≤3,该函数的最大值是,最小值是.求二次函数的最值问题,我们应注意什么?y=-(x–2)2+5.-11451y最大值=-2.y最小值=-4.注意自变量的取值范围.如图,一座拱桥的纵截面是抛物线的一段,拱桥的跨度是4.9m,水面宽4m时,拱顶离水面2m,水面宽度变化时,拱顶离水面高度怎样变化?动脑筋知识探究知识探究yxO知识探究知识探究拱桥的纵截面是抛物线的一部分,应当是某个二次函数的图象,因此可以建立二次函数模型来解决问题.知识探究知识探究1.怎样确定这个二次函数的解析式?先建立直角坐标系,然后找到抛物线上几个点的坐标,就可以确定这个二次函数的解析式.2.怎样建立坐标系简便?以拱顶为原点,对称轴为y轴,建立坐标系,因为抛物线顶点为原点,可设此二次函数解析式为y=ax2.yoxAB如图建立直角坐标系,则顶点坐标为如图建立直角坐标系,则顶点坐标为(0,0)(0,0).221xy所以,这条抛物线的解析式为:.解:解:设这条抛物线表示的二次函数关系式为:y=ax2.由于水面宽为4米时,拱顶离水面2米,则A点坐标为(2,-2).所以-2=a×22.解得yoxAB(2,-2)知识探究知识探究由于拱桥的跨度为4.9米时,因此-2.45≤x≤2.45.1=.2a-你还有其它建立坐标系的方法吗?此时函数的解析式又是怎样的?xyOA(2,0)P(0,2)想一想:当水面宽4.6米时,拱顶离水平几米?知识探究知识探究2.645米y=-0.5x2+2.1.如图是某抛物线形悬索桥的截面示意图,已知悬索桥两端主塔高150m,主塔之间的距离为900m,试建立适当的直角坐标系,求出该抛物线形桥所对应的二次函数表达式.练习900m150m150m900m设该抛物线形桥所对应的二次函数表达式为y=ax2.解:如图,以悬索桥的中点为原点,抛物线形桥的对称轴为y轴建立直角坐标系.Oxy4502·a=150解得1.1350a(-450≤x≤450)答:该抛物线形桥所对应的二次函数表达式为y=213501x知识探究知识探究建立二次函数模型解决实际问题的基本步骤是什么?议一议:实际问题建立二次函数模型利用二次函数的图象和性质求解实际问题的解如图所示,用8m长的铝材做成一个日字形窗框.试问:窗框的宽和高各为多少时,窗框的透光面积S(m2)最大?最大面积是多少?(假设铝材的宽度不计)解:设窗框的宽为xm,则高为.83m2x-动脑筋238xxS这时窗框的高为4833=2m.2×()-答:当窗框的宽为,高为2m时,窗框的透光面积最大,最大透光面积为4m3.28m33834232x当时,S最大=,34x3838(0