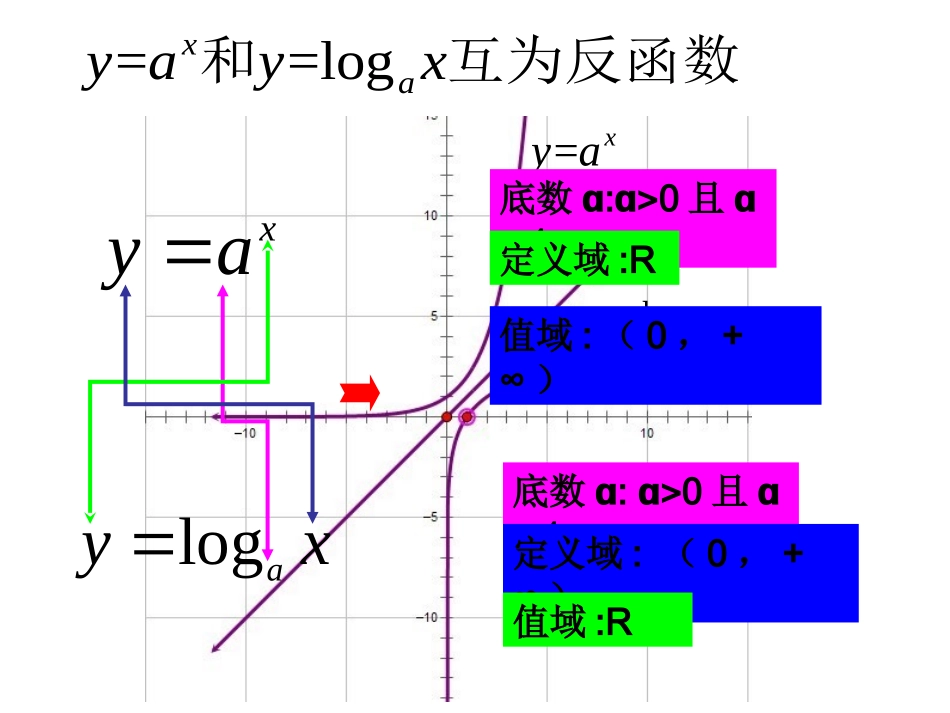
一、复习指数函数、对数函数和幂函数图形性质函数底数图像定义域RR值域RR定义域对值域当x>0时,y>1,当x<0时,00时,01,当01时,y>0,当01,当x>1时,y<0图形性质共同点过定点(0,1)过定点(1,0)单调性在区间R上为增函数在区间R上为减区间在(0,+∞)上为增函数在(0,+∞)上为减函数奇偶性不具有奇偶性不具有奇偶性极值无最大值和最小值极值=xya=logayx0<<1a>1a0<<1a>1ayx0y=1(0,1)yx(0,1)y=100xy0xy(1,0)(1,0)0,()0,()0,()0,()==logxayayx和互为反函数=xya=logayx=yxxyalogxay底数:ɑɑ0且ɑ1定义域:R值域:(0,+∞)底数:ɑɑ0且ɑ1定义域:(0,+∞)值域:R>0(0,+)<0(0,+)()()fxfaax,在区间为增函数单调性,,在区:间为减函数。()()()afxafxafx奇偶性:为偶数,偶函数;为奇数,奇函数为分数,若分母为偶数,不具有奇偶性>01,10,0<01()(,)1aafxfx,过定点()、(),,过定点(共同点:)。.在第一象限,沿箭头方向,指数越小二、应用示例31-log202215-0.01--+3+lg2)+lg5lg2+lg58【例】计算()(1-21--221=-1+2+lg2(lg2+lg5)+lg5100=10+1+lg2+lg5=10+1+1=12解:原式1【练习】计算41log16931log9+log27+4541082log27=,54=3,,log81baab【练习】已知如何用表示?b54545454108545454545454=3,log3=log81log27+log3log81==log108log54+log2++==1+log54-log272-bababa解:122314382(1)lg2=,lg3=,,log5(2)log3=,log7=,,log56abababab【练习】课本P已知如何用表示?已知如何用表示?22+1211()=-1212()=log(-1+33()=log3-2xxfxfxxfxxnnnnnnnnnnnnnn01111-102221=20()[,+)xxxyxfx解:()即又在区间R上为减函数即的定义域为02222-1>>12log(-1)+30log(-1)-3>1>119log(-1)log8899()1)(,+)88xoxxxxxxxfx()的定义域为(,1>2+1>0232+1103-2>02>32(),+)3xxxxxxfx()的定义域为(32411()=log(3-22()=log(2-)3()=log(1-)aafxxfxxfxx【练习】求定义域P82())()()