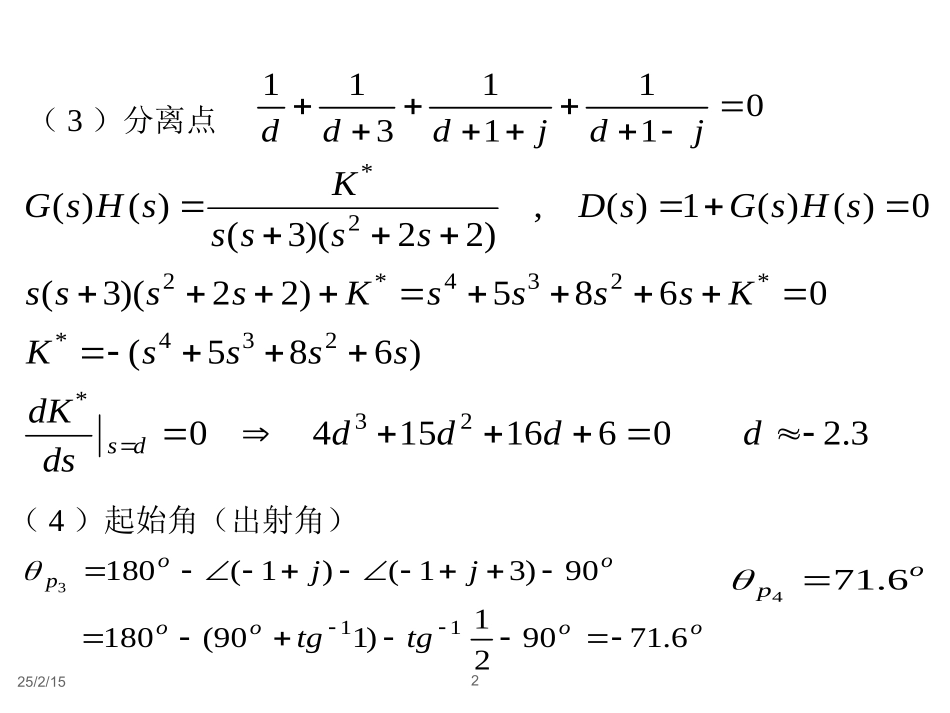画根轨迹例题VIP免费

25/2/151)22)(3()()(2*ssssKsHsG例5设系统开环传递函数试绘制闭环系统大致的根轨迹。解（1）无开环零点，开环极点在实轴上根轨迹[-3，0]。（2）有4条分支趋向无穷远处。渐近线的夹角与交点jppp1,3,04,32125.141130135,454180)12(jjkaoooa25/2/152（3）分离点01111311jdjddd3.206161540)685(0685)22)(3(0)()(1)(,)22)(3()()(23*234**234*22*dddddsdKssssKKssssKsssssHsGsDssssKsHsGds（4）起始角（出射角）ooooooptgtgjj6.719021)190(18090)31()1(180113op6.71425/2/153（5）与虚轴的交点运用劳斯判据0685)(0)()(1)(*234KsssssDsHsGsD*0**23*4034/)25204(5686581KsKsKssKs由第一列、第四行元素为零16.8025204**KK由辅助方程095.1016.8)568(2,12jss25/2/1540j13.23095.1j095.1j例已知系统开环传函如下，试求出根轨迹与虚轴的交点及相应的开环根轨迹增益的临界值。c*cK令s=jω并代入特征方程得*G(s)H(s)(s1)(s2)(s3)K32*s6s11s60K32*jω6ωj11ω60K其虚部和实部方程分别为3*211ωω066ω0K解系统特征方程是c*ω1160cK解方程组得：例已知系统的开环传递函数如下试绘制该系统的根轨迹图。⑵共有4个根轨迹分支，连续且对称于实轴。*2()()(4)(420)KGsHsssss⑶实轴上的根轨迹是实轴上由0到-4的线段。解⑴根轨迹起始于开环极点p1=0、p2=-4、p3=-2+4j、p4=-2-4j；终止于4个无限零点（没有有限零点)。0-4j*0K*0K*0K*0K渐近线在横轴上的公共交点为渐近线与横轴的夹角为k取0、l、2、3时，分别为450、1350、2250、3150。(4)渐近线:114242424nmijijapzjjnma210,1,2,34kk0-2-4j*0K*0K*0K*0K(5)分离点和分离角1111042424dddjdj经整理可得2(2)(410)0ddd求解上式可得三个分离点为123222.4522.45ddjdj分离角(21)0,1dkkll=2时，0900-2-4j*0K*0K*0K*0K1d3d2d090090(6)起始角311(21)jijimnpzpppjjjik复数极点p3和p4的起始角0-4j3p1p2p4p060090012011(21)()ijijimnpzpppjjjik4090p000(21)(6090120)k0900-2-4j*0K*0K*0K*0K1d3d2d090090090090(7)与虚轴的交点2*(4)(420)0ssssK用s=jω代入特征方程并令方程两边实部和虚部分别相等：42*336(808)0Kj42*33608080K*103.25K0-2-4j*0K*0K*0K*0K*K*K*K*K*10(3.25)K*10(3.25)K1d3d2d090090090090