对数与对数函数-三角函数-和差化积公式及其推导过程VIP免费

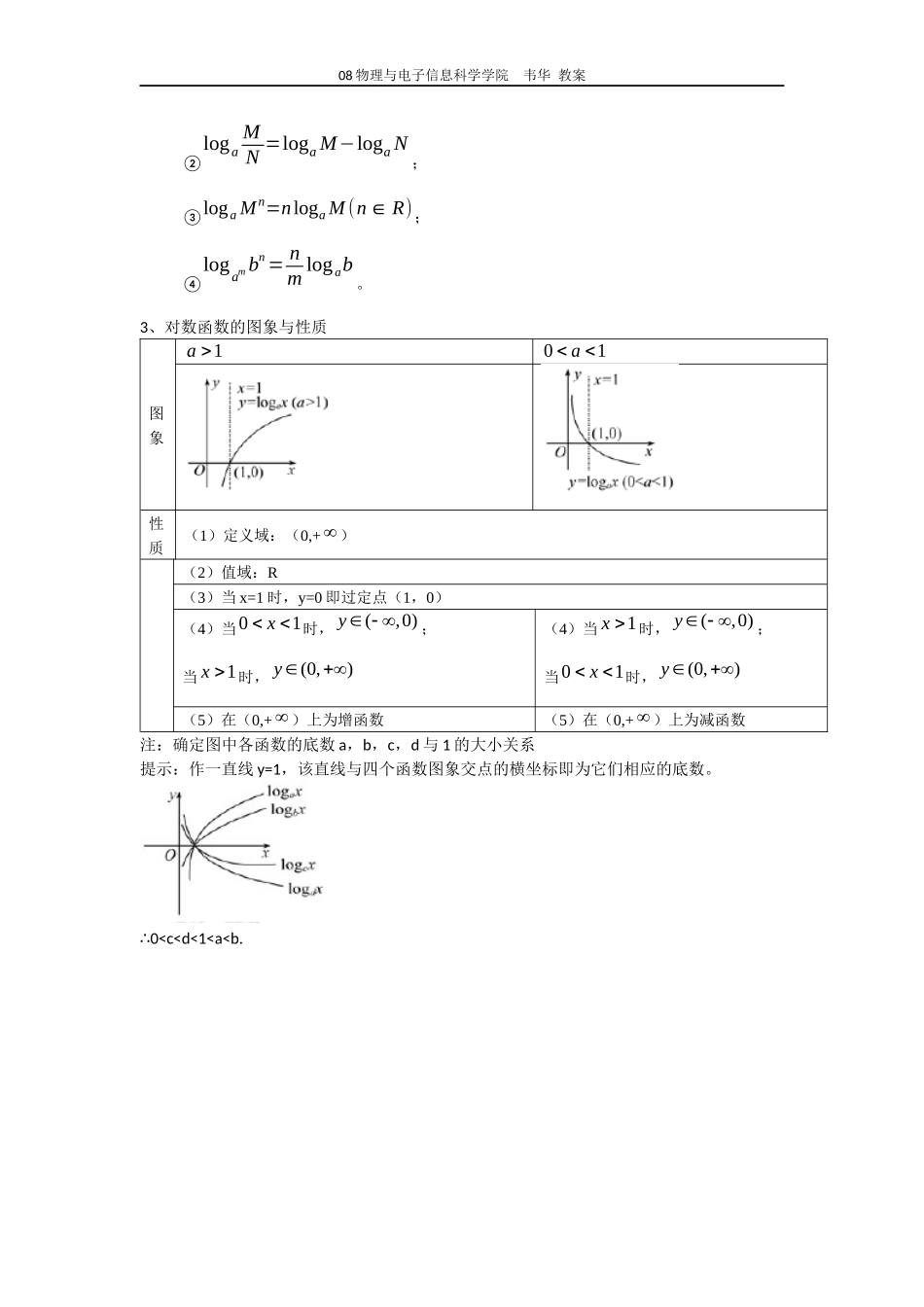
08物理与电子信息科学学院韦华教案lg2=0.3010lg3=0.4771lg5=0.6990lg7=0.84512．有理数指数幂（1）幂的有关概念①正数的正分数指数幂:;②正数的负分数指数幂:③0的正分数指数幂等于0,0的负分数指数幂没有意义.注：分数指数幂与根式可以互化，通常利用分数指数幂进行根式的运算。（2）有理数指数幂的性质①aras=ar+s(a>0,r、s∈Q);②(ar)s=ars(a>0,r、s∈Q);③(ab)r=arbs(a>0,b>0,r∈Q);.3．指数函数的图象与性质y=axa>100时，y>1;x<0时,00时，01(3)在（-，+）上是增函数（3）在（-，+）上是减函数注：如图所示，是指数函数（1）y=ax,（2）y=bx,（3）,y=cx（4）,y=dx的图象，如何确定底数a,b,c,d与1之间的大小关系？08物理与电子信息科学学院韦华教案提示：在图中作直线x=1，与它们图象交点的纵坐标即为它们各自底数的值，即c1>d1>1>a1>b1,c>d>1>a>b∴。即无论在轴的左侧还是右侧，底数按逆时针方向变大。（二）对数与对数函数1、对数的概念（1）对数的定义如果(01)xaNaa且，那么数x叫做以a为底，N的对数，记作logNax，其中a叫做对数的底数，N叫做真数。（2）几种常见对数对数形式特点记法一般对数底数为a0,1aa且logNa常用对数底数为10lgN自然对数底数为elnN2、对数的性质与运算法则（1）对数的性质（0,1aa且）：①1log0a，②log1aa，③logNaaN，④logNaaN。（2）对数的重要公式：①换底公式：loglog(,1,0)logNNabbaabN均为大于零且不等于；②1loglogbaab。（3）对数的运算法则：如果0,1aa且，0,0MN那么①loga(MN)=logaM+logaN；08物理与电子信息科学学院韦华教案②logaMN=logaM−logaN；③logaMn=nlogaM(n∈R)；④logambn=nmlogab。3、对数函数的图象与性质图象1a01a性质（1）定义域：（0,+）（2）值域：R（3）当x=1时，y=0即过定点（1，0）（4）当01x时，(,0)y；当1x时，(0,)y（4）当1x时，(,0)y；当01x时，(0,)y（5）在（0,+）上为增函数（5）在（0,+）上为减函数注：确定图中各函数的底数a，b，c，d与1的大小关系提示：作一直线y=1，该直线与四个函数图象交点的横坐标即为它们相应的底数。0