九年级数学几何证明方法的基本定式(中位线)人教版试卷VIP免费

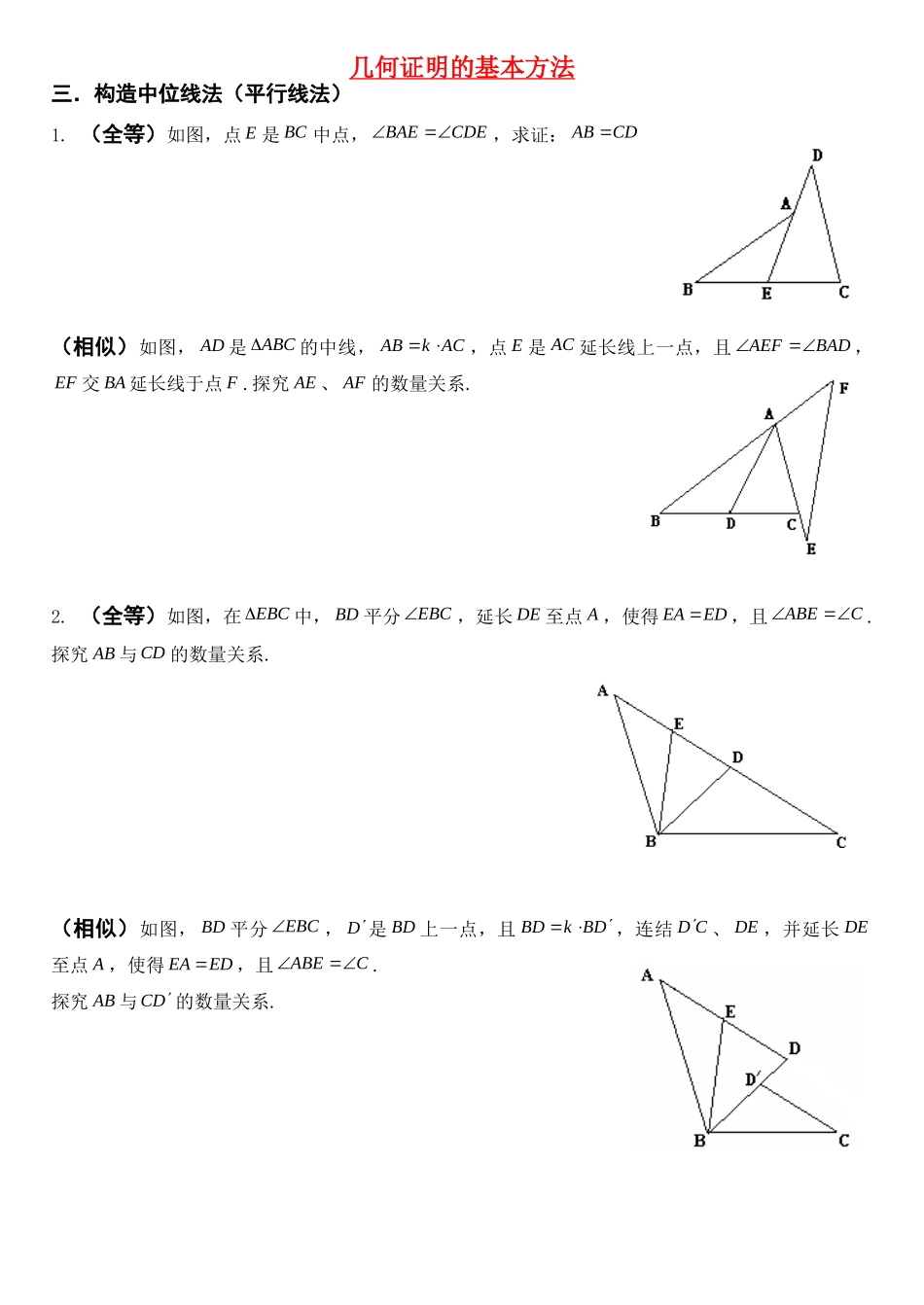
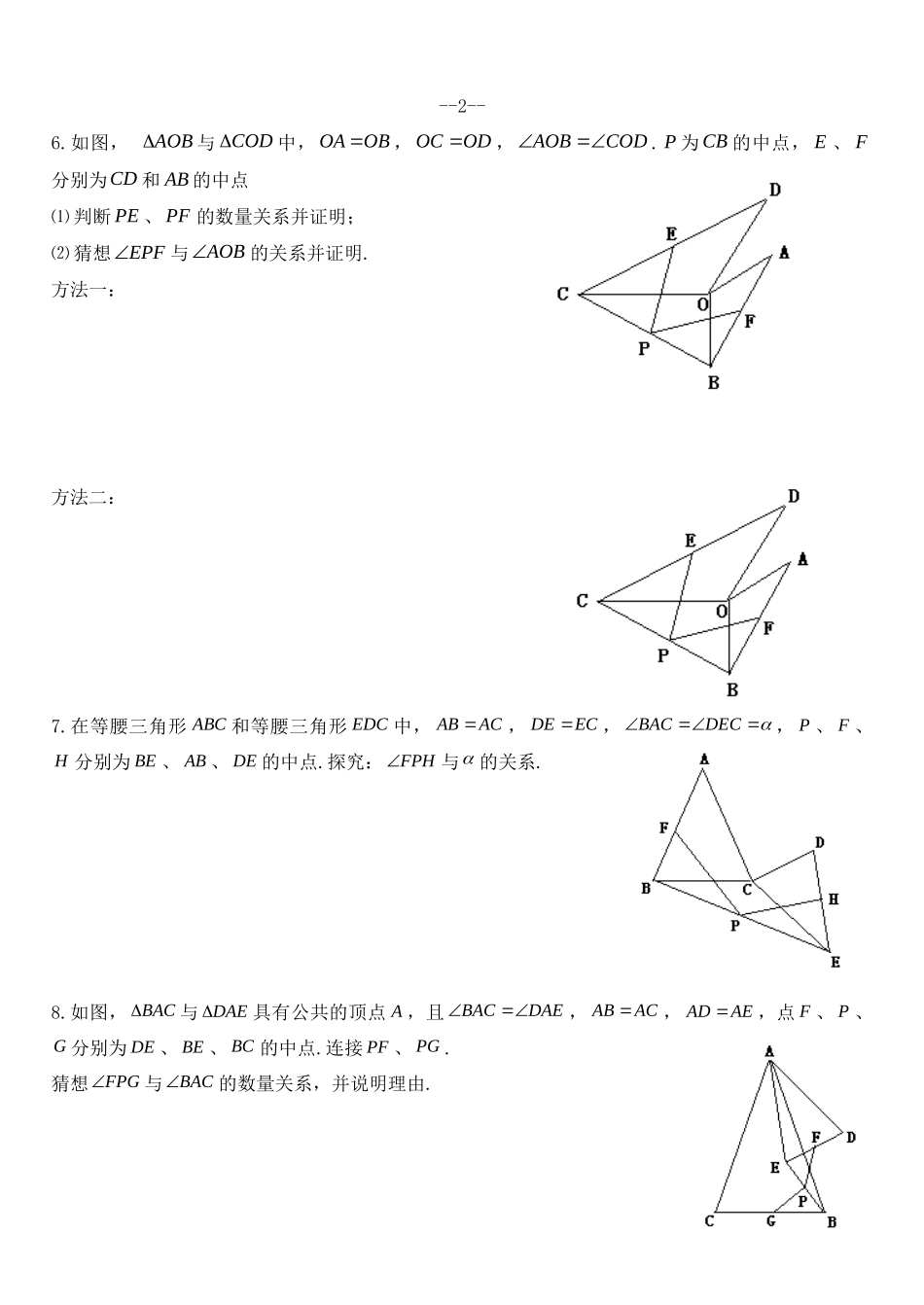
几何证明的基本方法三．构造中位线法（平行线法）1.（全等）如图，点E是BC中点，CDEBAE，求证：CDAB（相似）如图，AD是ABC的中线，ACkAB，点E是AC延长线上一点，且BADAEF，EF交BA延长线于点F.探究AE、AF的数量关系.2.（全等）如图，在EBC中，BD平分EBC，延长DE至点A，使得EDEA，且CABE.探究AB与CD的数量关系.（相似）如图，BD平分EBC，D是BD上一点，且DBkBD，连结CD、DE，并延长DE至点A，使得EDEA，且CABE.探究AB与DC的数量关系.--1--3.如图，四边形ABCD，CDAB，E、F分别为边AD、BC的中点，FE的延长线分别交CD、BA的延长线于G、H.求证：CGFH4.如图，在ABC中，E是BC的中点，在AC上有一点D，且满足ABCD，F是AD的中点，连结EF并延长交BA的延长线于点G.求证：AFAG5.（全等）如图，等腰直角ABC与等腰直角BDE，P为CE中点，连接PA、PD.探究PA、PD的关系.（相似）如图，ABC与BDE中，90BDECAB，ABkAC，DBkDE，P为CE中点，连接PA、PD.探究PA、PD的数量关系.--2--6.如图，AOB与COD中，OBOA，ODOC，CODAOB.P为CB的中点，E、F分别为CD和AB的中点⑴判断PE、PF的数量关系并证明；⑵猜想EPF与AOB的关系并证明.方法一：方法二：7.在等腰三角形ABC和等腰三角形EDC中，ACAB，ECDE，DECBAC，P、F、H分别为BE、AB、DE的中点.探究：FPH与的关系.8.如图，BAC与DAE具有公共的顶点A，且DAEBAC，ACAB，AEAD，点F、P、G分别为DE、BE、BC的中点.连接PF、PG.猜想FPG与BAC的数量关系，并说明理由.--3--9.如图，BAC与DAE具有公共的顶点A，且DAEBAC，ACkAB，ADkAE，点F、P、G分别为DE、BE、BC的中点.连接PF、PG.猜想FPG与BAC的数量关系，并说明理由.10.⑴如图1，操作：把正方形CGEF的对角线CE放在正方形ABCD的边BC的延长线上（BCCG）取线段AE的中点P.探究：线段PD、PF的关系，并加以证明.⑵如图2，将正方形CGEF绕点C旋转任意角度后，其他条件不变.探究：线段PD、PF的关系，并加以证明.11.如图，ABC与DBE中，90DEBACB，BCkAC，BEkDE，P为AD的中点.⑴探究PC、PE的数量关系；⑵探究CPE与CAB的关系.--4--