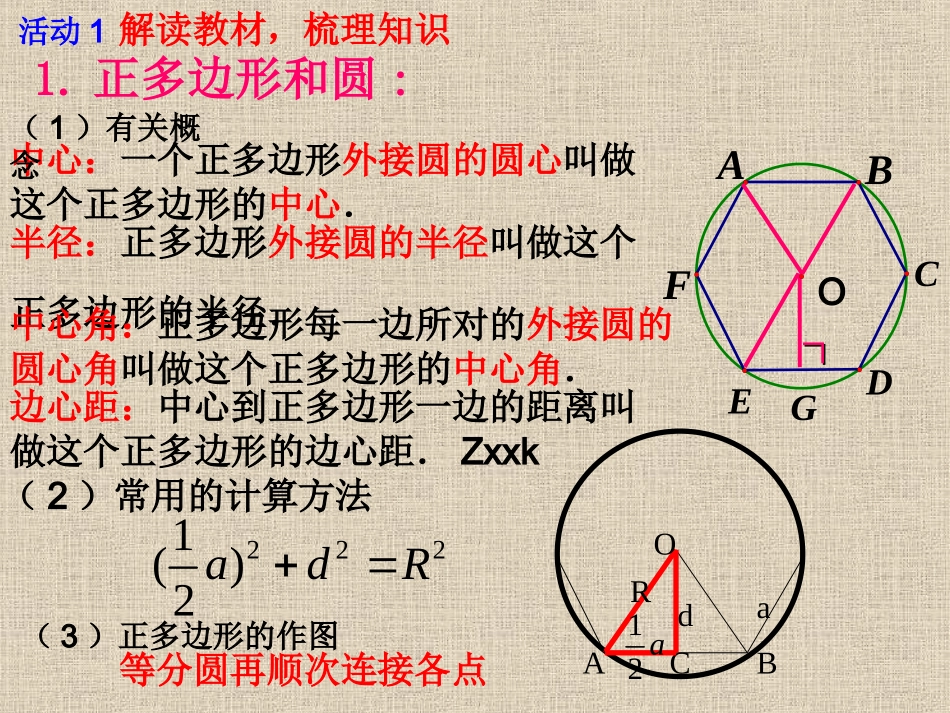
第二十四章圆第3课时第二十四章第二十四章圆复习圆复习1.正多边形和圆:半径:正多边形外接圆的半径叫做这个正多边形的半径.zxxk中心:一个正多边形外接圆的圆心叫做这个正多边形的中心.中心角:正多边形每一边所对的外接圆的圆心角叫做这个正多边形的中心角.边心距:中心到正多边形一边的距离叫做这个正多边形的边心距.ZxxkOABFDCEG活动1解读教材,梳理知识∟∟OABCRd12aa2221()2adR(2)常用的计算方法(3)正多边形的作图(1)有关概念等分圆再顺次连接各点(1)圆的周长和面积公式周长C=2πr面积S=πr2(2)弧长的计算公式zxxkl=180nπr(3)扇形的面积公式S=360nπr2或=12lrS.Orr活动1解读教材,梳理知识2.弧长和扇形面积:llnn高h母线a半径raS侧=πraS全=πra+πr2侧面底面活动1解读教材,梳理知识3.圆锥的展开图:活动2例题精析,巩固深化命题角度:1.正多边形和圆有关的概念2.正多边形的有关计算[2011·连云港]如图32-2,在正五边形ABCDE中,对角线AD、AC与EB分别交于点M、N.下列说法错误..的是()A.四边形EDCN是菱形B.四边形MNCD是等腰梯形C.△AEM与△CBN相似D.△AEN与△EDM全等图32-2[解析]正五边形ABCDE的每一个内角是108°,图中△AED、△AEB、△ABC都是全等的底角为36°的等腰三角形,△AEN、△DEM、△BCN、△ABM都是全等的等腰三角形,顶角为36°,故选项A、B、D正确,C不正确.C活动2例题精析,巩固深化命题角度:1.已知圆心角和半径求弧长2.利用转化思想求弧长zxxk[2011·滨州]如图32-3在△ABC中,∠B=90°,∠A=30°,AC=4cm,将△ABC绕顶点C顺时针方向旋转至△A?B?C的位置,且A、C、B?三点在同一条直线上,则点A所经过的最短路线的长为()A.43cmB.8cmC.163πcmD.83πcm图32-3[解析]D点A所经过的最短路线是以C点为圆心,以AC为半径,圆心角为120°的扇形弧长,120180π×4=83πcm.D拓展提高83π[2010·台州]如图32-5,菱形ABCD中,AB=2,∠C=60°,菱形ABCD在直线l上向右作无滑动的翻滚,每绕着一个顶点旋转60°叫一次操作,则经过36次这样的操作菱形中心O所经过的路径总长为(结果保留π)_______.图32-5如图32-4所示,边长为2的等边三角形木块,沿水平线l滚动,则A点从开始至结束所走过的路线长为________(结果保留准确值).图32-4(83+4)π命题角度:1.已知扇形的半径和圆心角,求扇形的面积2.已知扇形的弧长和半径,求扇形的面积[2010·新疆]圆心角都是90°的扇形AOB与扇形COD如图32-6所示那样叠放在一起,连接AC、BD.(1)求证:△AOC≌△BOD;(2)若AO=3cm,OC=1cm,求阴影部分的面积.图32-6活动2例题精析,巩固深化[解析](1)把△AOC旋转到△BOD,可知这两个三角形全等;(2)把阴影面积化为两个扇形面积的差.命题角度:1.圆锥的母线长、底面半径等计算2.圆锥的侧面展开图的相关计算[2011·宁波]如图32-7,Rt△ABC中,∠ACB=90°,AC=BC=22,若把Rt△ABC绕边AB所在直线旋转一周,则所得的几何体的表面积为()A.4πB.42πC.8πD.82π图32-7活动2例题精析,巩固深化求不规则图形的面积,常转化为易解决问题的基本图形,然后求出各图形的面积,通过面积的和或差求出结果.D命题角度:1.用化归思想解决生活中的实际问题2.综合利用所学知识解决实际问题如图32-8中的线CD表示某条公路的一段,其中AMB是一段圆弧,AC、BD是线段,且AC、BD分别与圆弧AMB相切于点A、B,线段AB=180m,∠ABD=150°.(1)画出圆弧AMB的圆心O;(2)求A到B这段弧形公路的长.图32-8活动2例题精析,巩固深化解:(1)如图,过A作AO⊥AC,过B作BO⊥BD,AO与BO相交于O,O即为圆心.(2) AO、BO都是圆弧AMB的半径,O是其圆心,∴∠OBA=150°-90°=60°.∴△AOB为等边三角形.∴AO=BO=AB=180.∴弧AB=π×60×180180=60π(m).∴A到B这段弧形公路的长为60πm.活动2例题精析,巩固深化活动3总结反思拓展升华1.复习了哪些数学知识?这些知识在解决圆的问题时有哪些作用?2.在解决问题时运用了哪些数学思想方法?圆中有哪些常见的辅助线?活动4自我检测1.如图,当半径为30cm的转动轮转过120°时,传送带上的物体A平移的距离为______.A3.如图,AB...