1.5.3定积分的概念VIP免费

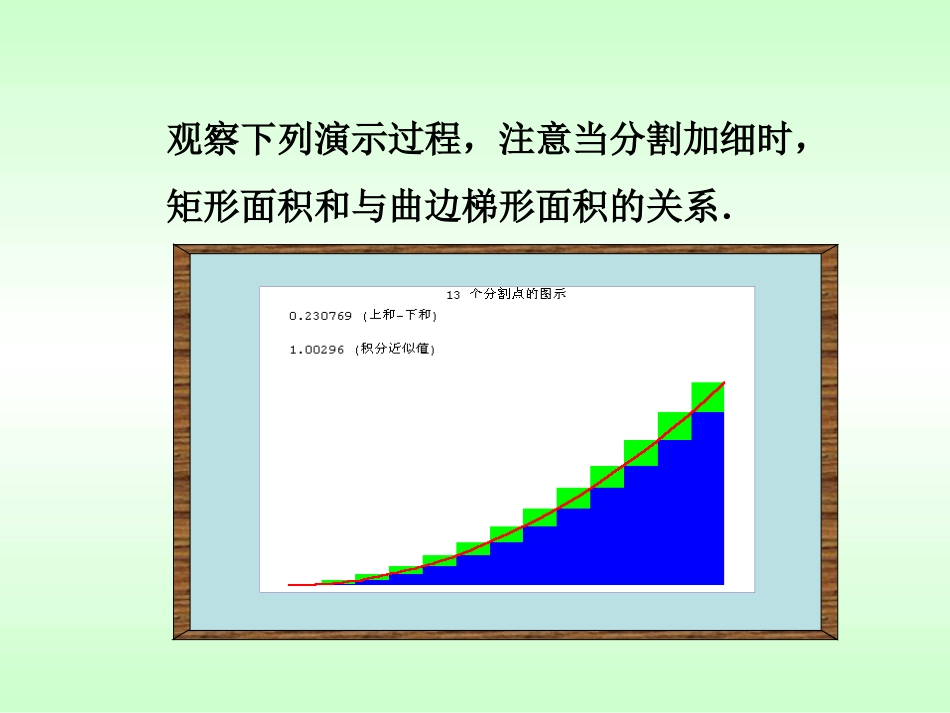
abxyo观察下列演示过程，注意当分割加细时，矩形面积和与曲边梯形面积的关系．观察下列演示过程，注意当分割加细时，矩形面积和与曲边梯形面积的关系．观察下列演示过程，注意当分割加细时，矩形面积和与曲边梯形面积的关系．观察下列演示过程，注意当分割加细时，矩形面积和与曲边梯形面积的关系．观察下列演示过程，注意当分割加细时，矩形面积和与曲边梯形面积的关系．观察下列演示过程，注意当分割加细时，矩形面积和与曲边梯形面积的关系．观察下列演示过程，注意当分割加细时，矩形面积和与曲边梯形面积的关系．观察下列演示过程，注意当分割加细时，矩形面积和与曲边梯形面积的关系．观察下列演示过程，注意当分割加细时，矩形面积和与曲边梯形面积的关系．观察下列演示过程，注意当分割加细时，矩形面积和与曲边梯形面积的关系．观察下列演示过程，注意当分割加细时，矩形面积和与曲边梯形面积的关系．观察下列演示过程，注意当分割加细时，矩形面积和与曲边梯形面积的关系．观察下列演示过程，注意当分割加细时，矩形面积和与曲边梯形面积的关系．求由连续曲线yf(x)对应的曲边梯形面积的方法(2)以直代曲:任取i[xi1,xi]，第i个小曲边梯形的面积用高为f(i)而宽为x的小矩形面积f(i)x近似之。(3)逼近:如果⊿x无限趋近于0时,Sn无限趋近于常数S（3）作和：取n个小矩形面积的和作为曲边梯形面积S的近似值：xiy=f(x)xyObaxi+1ix1()nniiSfx(1)分割:在区间[0,1]上等间隔地插入n-1个点,将它等分成n个小区间:每个小区间宽度⊿xban11211,,,,,,,,,iinaxxxxxxb一、定积分的定义11()()nniiiibafxfnn小矩形面积和S=如果当即n∞时，Sn的无限接近某个常数s，这个常数为函数f(x)在区间[a,b]上的定积分，记作baf(x)dx，即f(x)dxf(i)xi。从求曲边梯形面积S的过程中可以看出,通过“四步曲”:分割---以直代曲----作和------逼近得到解决.0←x▽定积分的定义：定积分的相关名称：———叫做积分号，f(x)——叫做被积函数，f(x)dx—叫做被积表达式，x———叫做积分变量，a———叫做积分下限，b———叫做积分上限，[a,b]—叫做积分区间。1()()(0)niibafxdxfnnba即Oabxy)(xfy积分下限积分上限badxxf)(被积函数积分变量Sbaf(x)dx；按定积分的定义，有(1)由连续曲线yf(x)(f(x)0)，直线xa、xb及x轴所围成的曲边梯形的面积为(2)设物体运动的速度vv(t)，则此物体在时间区间[a,b]内运动的距离s为sbav(t)dt。定积分的定义：Oab()vvttv1()()(0)niibafxdxfnnba即(3)变力作功问题可表示为badxxFW)(112001()3Sfxdxxdx根据定积分的定义右边图形的面积为1xyOf(x)=x213S1SD2SD2()2vtt=-+Ovt12gggggg3SDjSDnSD1n2n3njn1nn-4SD112005()(2)3Svtdttdt根据定积分的定义左边图形的面积为baf(x)dxbaf(t)dtbaf(u)du。说明：(1)定积分是一个数值,它只与被积函数及积分区间有关，而与积分变量的记法无关，即（2）定义中区间的分法和i的取法是任意的.baf(x)dxbaf(x)dx-(3)特别地，当ab时，有baf(x)dx0。（4）1.由曲线y=x2+1与直线x=1,x=3及x轴所围成的曲边梯形的面积,用定积分表示为____________.223sintdt2.中,积分上限是___,积分下限是___,积分区间是______二、举例dxx)1(2312-2[-2,2]3.定积分=__________.211)dx(x25.__________4dx4.定积分318思考:函数在区间[a,b]上的定积分能否为负的?定积分.____________121)dx(x定积分=__________.211)dx(xbAoxyay=f(x)S三.定积分的几何意义.（1）当f(x)≥0，定积分badxxf)(的几何意义就是曲线y=f(x)直线x=a，x=b，y=0所围成的曲边梯形的面积baSf(x)dx:即(2)当函数f(x)0，x[a,b]时定积分几何意义badxxf)(Sdxxfba)(即就是位于x轴下方的曲边梯形面积的相反数.oxyaby=f(x)S(3)当函数f(x)在x[a,b]有正有负时,定积分几何意义badxxf)(321baSSSf(x)dx即就是图中几个曲边图形面积的代数和,(x轴上方面积取正号,...