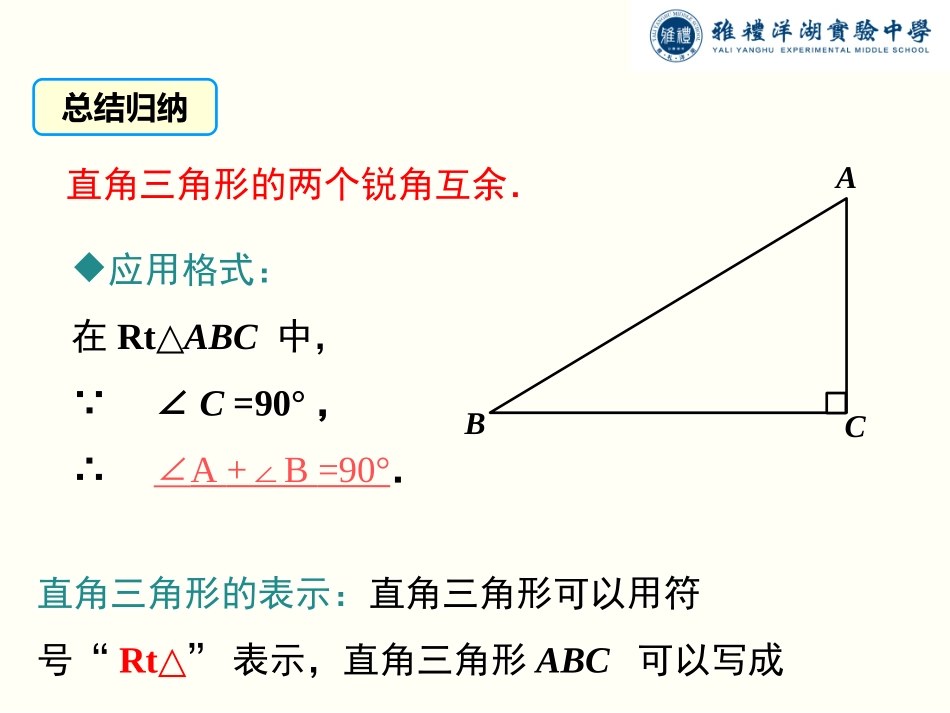
——雅礼洋湖实验中学数学备课组贺添喜1直角三角形的性质和判定问题:如图,在△ABC中,∠C=90°,两锐角的和等于多少呢?在△ABC中,因为∠C=90°,由三角形内角和定理,得∠A+∠B+C∠=180°,即∠A+∠B=90°.在△ABC中,因为∠C=90°,由三角形内角和定理,得∠A+∠B+C∠=180°,即∠A+∠B=90°.思考:由此,你可以得到直角三角形有什么性质呢?直角三角形的性质一ABC直角三角形的两个锐角互余.应用格式:在Rt△ABC中,∵∠C=90°,∴∠A+∠B=90°.直角三角形的表示:直角三角形可以用符号“Rt△”表示,直角三角形ABC可以写成Rt△ABC.总结归纳方法一(利用平行的判定和性质):∵∠B=∠C=90°,∴AB∥CD,∴∠A=∠D.方法二(利用直角三角形的性质):∵∠B=∠C=90°,∴∠A+∠AOB=90°,∠D+∠COD=90°.∵∠AOB=∠COD,∴∠A=∠D.oDCBA例1(1)如图,∠B=∠C=90°,AD交BC于点O,∠A与∠D有什么关系?图典例精析解:∠A=∠C.理由如下:∵∠B=∠D=90°,∴∠A+∠AOB=90°,∠C+∠COD=90°.∵∠AOB=∠COD,∴∠A=∠C.(2)如图,∠B=∠D=90°,AD交BC于点O,∠A与∠C有什么关系?请说明理由.oDCBA图思考:通过前面的例题,你能画出这些题型的基本图形吗?基本图形∠A=∠C∠A=∠D总结归纳oDCBAoDCBA例2如左图,在△ABC中,ADBC⊥于点D,CEAB⊥于点E.(1)猜测∠1与∠2的关系,并说明理由;(2)如果∠BAC是钝角,如右图,(1)中的结论是否还成立?1.具备下列条件的△ABC中,不是直角三角形的是()A.∠A+∠B=∠CB.∠A-∠B=∠CC.∠A:∠B:∠C=1:2:3D.∠A=∠B=3∠CD当堂练习问题:有两个角互余的三角形是直角三角形吗?如图,在△ABC中,∠A+∠B=90°,那么△ABC是直角三角形吗?在△ABC中,因为∠A+∠B+∠C=180°,又∠A+∠B=90°,所以∠C=90°.于是△ABC是直角三角形.在△ABC中,因为∠A+∠B+∠C=180°,又∠A+∠B=90°,所以∠C=90°.于是△ABC是直角三角形.直角三角形的判定二典例精析例3如图,∠C=90°,1=2∠∠,△ADE是直角三角形吗?为什么?ACBDE((12解:在Rt△ABC中,∠2+∠A=90°.∵∠1=2,∠∴∠1+∠A=90°.即△ADE是直角三角形.例4如图,ABCD∥,直线EF分别交AB,CD于点E,F,∠BEF的平分线与∠DFE的平分线相交于点P,试说明△EPF为直角三角形.解:∵AB∥CD,∴∠BEF+∠DFE=180°.∵EP为∠BEF的平分线,FP为∠EFD的平分线,∴∠PEF=∠BEF,∠PFE=∠DFE.∴∠PEF+∠PFE=(∠BEF+∠DFE)=90°.∴△EPF为直角三角形.12121.如图,一张长方形纸片,剪去一部分后得到一个三角形,则图中∠1+2∠的度数是________.90°2.如图,AB、CD相交于点O,AC⊥CD于点C,若∠BOD=38°,则∠A=________.52°第1题图第2题图当堂练习3.在△ABC中,若∠A=43°,∠B=47°,则这个三角形是____________.直角三角形4.如图所示,△ABC为直角三角形,∠ACB=90°,CD⊥AB,与∠1互余的角有()A.∠BB.∠AC.∠BCD和∠AD.∠BCDC7.如图,在直角三角形ABC中,∠ACB=90°,D是AB上一点,且∠ACD=∠B.求证:△ACD是直角三角形.证明:∵∠ACB=90°,∴∠A+∠B=90°,∵∠ACD=∠B,∴∠A+∠ACD=90°,∴△ACD是直角三角形.课堂小结直角三角形的性质与判定性质直角三角形的两个锐角互余判定有两个角互余的三角形是直角三角形