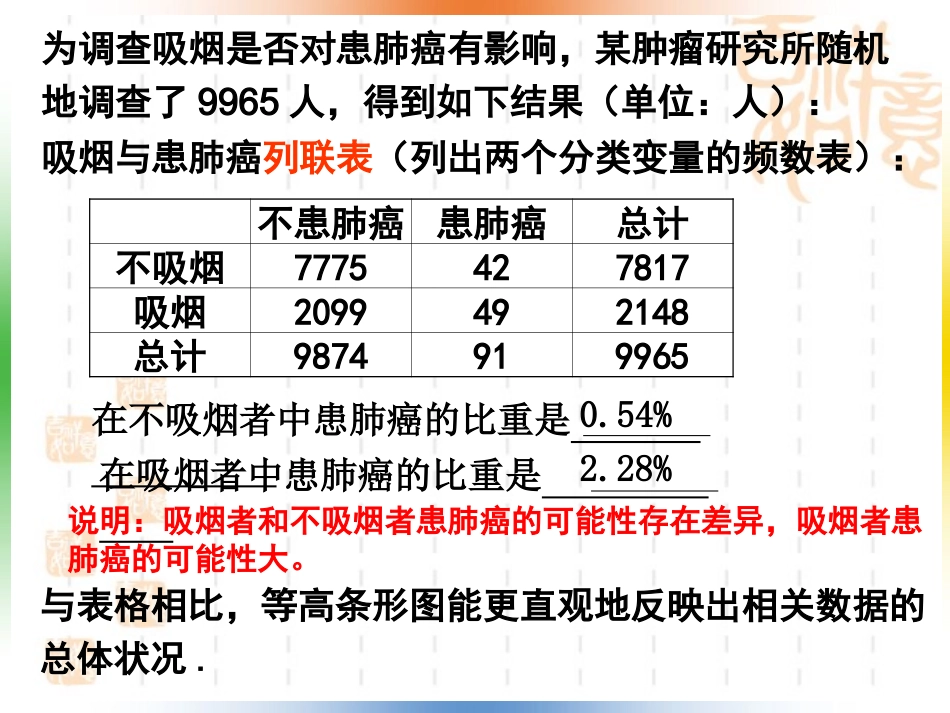
一:分类变量的概念:变量的不同“值”表示个体所属的不同类别,像这样的变量称为分类变量.在日常生活中,我们常常关心两个分类变量之间是否有关系:在统计学中,独立性检验就是检验两个分类变量是否有关系的一种统计方法。不患肺癌患肺癌总计不吸烟7775427817吸烟2099492148总计9874919965与表格相比,等高条形图能更直观地反映出相关数据的总体状况.为调查吸烟是否对患肺癌有影响,某肿瘤研究所随机地调查了9965人,得到如下结果(单位:人):吸烟与患肺癌列联表(列出两个分类变量的频数表):在不吸烟者中患肺癌的比重是在吸烟者中患肺癌的比重是说明:吸烟者和不吸烟者患肺癌的可能性存在差异,吸烟者患肺癌的可能性大。0.54%2.28%不吸烟吸烟00.10.20.30.40.50.60.70.80.91不吸烟吸烟患肺癌比例不患肺癌比例等高条形图等高条形图更清晰地表达了两种情况下患肺癌的比例.两个蓝色条的高分别表示不吸烟和吸烟样本中不患肺癌的频率。比较图中两个红色条的高可以发现,在吸烟样本中患肺癌的频率要高一些。这种判断是否可靠呢?下面通过统计分析回答这一问题。现在想要知道能够以多大的把握认为“吸烟与患肺癌有关”,为此先假设:H0:吸烟与患肺癌没有关系不患肺癌患肺癌总计不吸烟aba+b吸烟cdc+d总计a+cb+da+b+c+d把数字用字母代替,得到如下用字母表示的列联表:不患肺癌患肺癌总计不吸烟aba+b吸烟cdc+d总计a+cb+da+b+c+d假设H0:吸烟和患病之间没有关系用A表示不吸烟,B表示不患病设n=a+b+c+d即H0等价于P(AB)=P(A)P(B)()aPABn()abPAn()acPBn.bcad即.adbc应有不患肺癌患肺癌总计不吸烟aba+b吸烟cdc+d总计a+cb+da+b+c+d假设H0:吸烟和患病之间没有关系用A表示不吸烟,B表示不患病|ad-bc|越小,说明吸烟与患肺癌之间关系越弱;|ad-bc|越大,说明吸烟与患肺癌之间关系越强.为了使不同样本容量的数据有统一的评判标准,基于上述分析,我们构造一个随机变量若H0成立,即“吸烟与患肺癌没有关系”,则K2应很小.由列联表中数据,利用公式(1)计算得K2的观测值为:22()()()()()nadbcKabcdacbd(1)29965(777549422099)56.632.78172148987491k其中n=a+b+c+d为样本容量.怎样判断K2的观测值k是大还是小呢?这仅需要确定一个正数,当时就认为K2的观测值k大。此时相应于的判断规则为:0k0kk0k如果,就认为“两个分类变量之间有关系”;否则就认为“两个分类变量之间没有关系”。0kk0k----临界值在H0成立的情况下,统计学家估算出如下的概率:2(6.635)0.01PK也就是说,在H0成立的情况下,对随机变量K2进行多次观测,观测值超过6.635的频率约为0.01,是一个小概率事件.现在K2的观测值为56.632,远远大于6.635,所以有理由断定H0不成立,即认为“吸烟与患肺癌有关系”56.632k但这种判断会犯错误,犯错误的概率不会超过0.01,即我们有99%的把握认为“吸烟与患肺癌有关系”.利用随机变量K2来确定在多大程度上可以认为“两个分类变量有关系”的方法称为两个分类变量的独立性检验.独立性检验:P(≥x0)0.500.400.250.150.100.050.0250.0100.0050.001x00.4550.7081.3232.0722.7063.8415.0246.6357.87910.828210.828K26.635K22.706K0.1%把握认为A与B无关1%把握认为A与B无关99.9%把握认为A与B有关99%把握认为A与B有关90%把握认为A与B有关10%把握认为A与B无关例如临界值在实际应用中,要在获取样本数据之前通过下表确定临界值:0.500.400.250.150.100.4550.7081.3232.0722.7060.050.0250.0100.0050.0013.8415.0246.6367.87910.8280)k2P(K0k0k0)k2P(K具体作法是:(1)根据实际问题需要的可信程度确定临界值;(2)利用公式(1),由观测数据计算得到随机变量的观测值;(3)如果,就以的把握认为“X与Y有关系”;否则就说样本观测数据没有提供“X与Y有关系”的充分证据。0k2K0kk20(1())100%PKkk例1在某医院,因为患心脏病而住院的665名男性病人中,有214人秃顶;而另外772名不是因为患心脏病而住院的男性病人中有175人秃顶。能否在犯错误的概率不超过0.01的前提下认为秃顶与患心脏病有关系?0.050.0250.010.0050.0013.8415.0246....