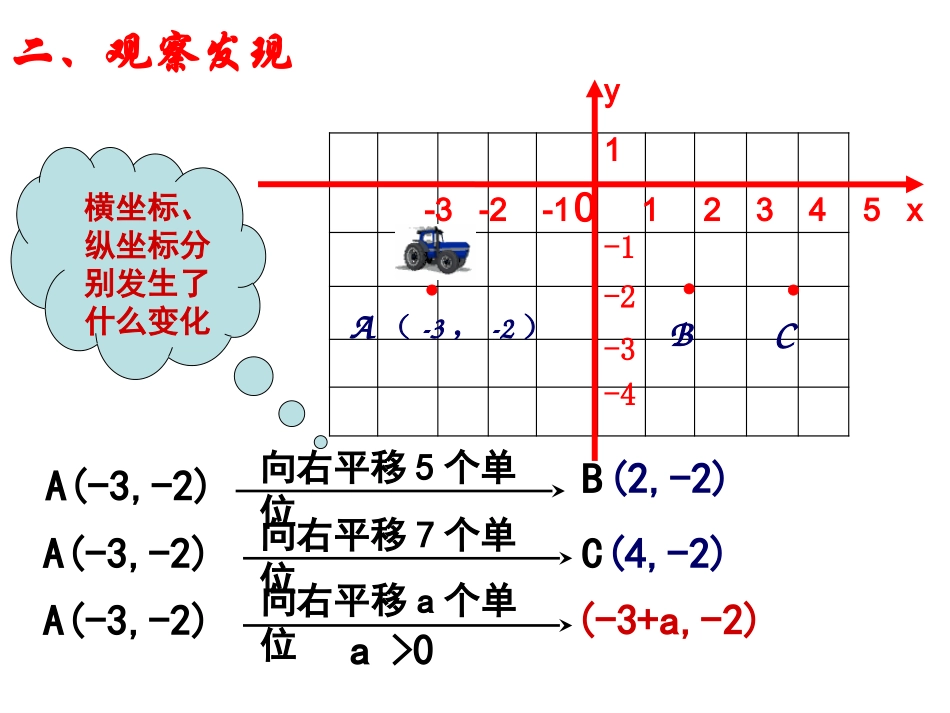
一、回顾旧知1.什么叫平移?2.图形的平移有哪些性质?在平面内,把一个图形沿某一方向移动一定的距离,会得到一个新图形.图形的这种移动叫做平移变换,简称平移.(1)新图形与原图形形状和大小完全相同;位置不同.(2)对应点的连线平行且相等.-3-2-112345xy01-1-2-3-4A(-3,-2)A(-3,-2)向右平移5个单位B(2,-2)BCA(-3,-2)向右平移7个单位C(4,-2)(-3+a,-2)A(-3,-2)向右平移a个单位a>0横坐标、纵坐标分别发生了什么变化●●●二、观察发现-4-3-2-112345xy01-1-2-3-4A(3,-2)A(3,-2)向左平移5个单位B(-2,-2)BCA(3,-2)向左平移7个单位C(-4,-2)(3-a,-2)A(3,-2)向左平移a个单位a>0●●●-4-3-2-112345xy04213-1A(3,-1)A(3,-1)向上平移3个单位B(3,2)BCA(3,-1)向上平移5个单位C(3,4)(3,-1+b)A(3,-1)向上平移b个单位b>0●●●-4-3-2-112345xy04213-1A(3,4)A(3,4)向下平移3个单位B(3,1)BCA(3,4)向下平移5个单位C(3,-1)(3,4-b)A(3,4)向下平移b个单位b>0●●●想一想,议一议•如果一个点的坐标可以表示为P(x,y),把这点向右(向左)平移a个单位,向上(向下)平移b个单位,你能把上述坐标的变化规律表示出来吗?把你的结论和其他同学进行交流。(1)左、右平移:向右平移a个单位()(2)上、下平移:原图形上的点(x,y),向左平移a个单位()原图形上的点(x,y),x+a,yx-a,y向上平移b个单位()原图形上的点(x,y),向下平移b个单位()原图形上的点(x,y),x,y+bx,y-b总结规律:图形平移与点的坐标变化间的关系左右平移,纵坐标不变,横坐标变化(左减右加)上下平移,横坐标不变,纵坐标变化(下减上加)口诀上下平移左右平移上加下减横不变左减右加纵不变1.将点A(3,2)向上平移2个单位长度,得到A’,则A’的坐标为______.2.将点A(3,2)向下平移3个单位长度,得到A’,则A’的坐标为______.3.将点A(3,2)向左平移4个单位长度,得到A’,则A’的坐标为______.4.将点A(3,2)向右平移2个单位长度,得到A’,则A’的坐标为______.(3,4)(3,-1)(-1,2)(5,2)三、巩固新知问题4如图,如何沿坐标轴方向平移A(-2,1)得到A1?点A先向右平移5个单位长度,再向下平移3个单位长度;或将点A先向下平移3个单位长度,再向右平移5个单位长度.巩固应用拓展延伸问题5如图4,正方形ABCD四个顶点的坐标分别是A(-2,4),B(-2,3),C(-1,3),D(-1,4),将正方形ABCD向下平移7个单位长度,再向右平移8个单位长度,两次平移后四个顶点相应变为点E,F,G,H.(1)点E,F,G,H的坐标分别是什么?问题5如图4,正方形ABCD四个顶点的坐标分别是A(-2,4),B(-2,3),C(-1,3),D(-1,4),将正方形ABCD向下平移7个单位长度,再向右平移8个单位长度,两次平移后四个顶点相应变为点E,F,G,H.(2)如果直接平移正方形ABCD,使点A移到点E,它和我们前面得到的正方形位置相同吗?1.把点M(1,2)平移后得到点N(1,-2)则平移的过程是:向下平移4个单位2.把点M(-3,1)平移后得到点N(-1,4)则平移的过程是:向右平移2个单位,再向上平移3个单位或:向上平移3个单位,再向右平移2个单位(1)将三角形ABC三个顶点的横坐标都减去6,纵坐标不变,分别得到点A1,B1,C1,点A1,B1,C1坐标分别是什么?并画出相应的三角形A1B1C1.探究发现合作交流问题2如图,三角形ABC三个顶点的坐标分别是:A(4,3),B(3,1),C(1,2).(2)三角形A1B1C1与三角形ABC的大小、形状和位置上有什么关系,为什么?(3)若三角形ABC三个顶点的横坐标都加5,纵坐标不变呢?探究发现合作交流问题2如图,三角形ABC三个顶点的坐标分别是:A(4,3),B(3,1),C(1,2).解:A1(-2,3),B1(-3,1),C1(-5,2),即三角形ABC向左平移了6个单位长度,因此所得三角形A1B1C1与三角形ABC的大小、形状完全相同.用类比的思想,把三角形ABC三个顶点的横坐标都加5,纵坐标不变,即三角形ABC向右平移了5个单位长度,因此所得三角形与三角形ABC的大小、形状完全相同.问题3如图,将三角形ABC三个顶点的纵坐标都减去5,横坐标不变,猜想:三角形A2B2C2与三角形ABC的大小、形状和位置上有什么关系?探究发现合作交流用类比的思想,探究得到三角形...