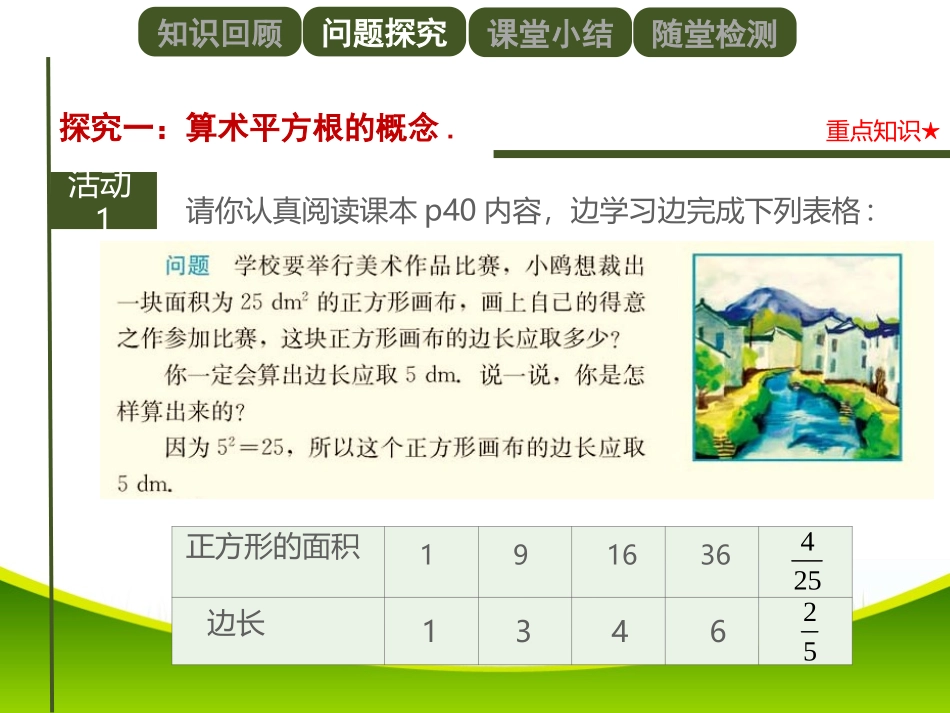
6.1平方根(第一课时)知识回顾问题探究课堂小结随堂检测(1)10~20之间整数的平方,你都记得哪些?11²=121,12²=144,13²=169,14²=196,15²=225,16²=256,17²=289,18²=324,19²=361.(2)若a是有理数,则一定是非负数.知识回顾问题探究课堂小结随堂检测请你认真阅读课本p40内容,边学习边完成下列表格:活动1探究一:算术平方根的概念.重点知识★正方形的面积191636边长425251346知识回顾问题探究课堂小结随堂检测已知“正方形面积求边长”的问题,实际上是“已知一个正数的平方,求这个正数”的问题,通过解决这个问题,我们就有了算术平方根的概念.活动1探究一:算术平方根的概念.重点知识★如3²=9,我们知道9是正数3的平方数,反过来,我们把正数3叫做9的算术平方根.算术平方根的概念:一般地,如果一个正数x的平方为a,即x²=a,那么正数x叫做a的算术平方根.知识回顾问题探究课堂小结随堂检测活动1探究一:算术平方根的概念.重点知识★算术平方根的表示方法:a的算术平方根记为,读作“根号a”或“二次根号a”,其中a叫做被开方数.a规定:0的算术平方根是0,记作.0知识回顾问题探究课堂小结随堂检测活动1探究二:求一个非负数的算术平方根重点、难点知识★▲初步运用:因为x²=a,所以x=(x≥0)a例1.求下列各数的算术平方根.(1)100(2)(3)0.0001(4)4964719解析:(1)因为10²=100,所以100的算术平方根是10,即.(2)因为,所以的算术平方根是,即.(3)因为0.01²=0.0001,所以0.0001的算术平方根是0.01,即.(4)因为==,所以的算术平方根是,即.719497=64849640.0001=0.012749=864100=1078169224371943741=99方法总结:带分数记得要先化成假分数;思考:观察比较上述各数的算术平方根的大小,由此你能得出什么结论?知识回顾问题探究课堂小结随堂检测活动1探究二:求一个非负数的算术平方根重点、难点知识★▲初步运用:因为x²=a,所以x=(x≥0)a思考:观察比较上述各数的算术平方根的大小,由此你能得出什么结论?结论:被开方数大的数算术平方根也大.这个结论对所有非负数都成立.即(a≥0);(a≤0)2aa2aa知识回顾问题探究课堂小结随堂检测活动2探究二:求一个非负数的算术平方根重点、难点知识★▲灵活运用:(a≥0);(a≤0)2aa方法总结:此类型题目应注意:(a≥0);(a≤0),需强调的是a=0时对两种情况都成立.2aa2aa2aa例2.求下列各式的值:(1)(2)(3)(4)40.164110211解析:(1)(2)(3)(4)22422111==1010100.16=0.44=22211=11=11知识回顾问题探究课堂小结随堂检测思考:-4有算术平方根吗?-9,-36,-49呢?任意一个负数有算术平方根吗?活动1探究三:算术平方根的性质:双重非负性负数不能写成某个数的平方,所以没有算术平方根.归纳:一个正数的算术平方根有1个;0的算术平方根是0;负数没有算术平方根.即:只有非负数有算术平方根,如果x=有意义,那么a≥0,x≥0.这就是算术平方根的双重非负性.a知识回顾问题探究课堂小结随堂检测巧用双重非负性活动2探究三:算术平方根的性质:双重非负性方法总结:巧妙运用x=有意义,则a≥0,x≥0,可以解决综合性较强的题目.a例2.若,求a、b的值.25730ab解析:因为,,所以要使它们的和等于0,则,.所以有5a+7=0,b-3=0即,.2570a30b2570a30b75a3b知识梳理知识回顾问题探究课堂小结随堂检测基础知识思维导图算术平方根为非负数被开方数为非负数非负性负数没有平方根0的平方根是0一个正数有两个平方根,它们互为相反数算术平方根性质定义平方根知识梳理知识回顾问题探究课堂小结随堂检测算术平方根的概念:一般地,如果一个正数x的平方为a,即x²=a,那么正数x叫做a的算术平方根.算术平方根的双重非负性:只有非负数有算术平方根,如果x=有意义,那么a≥0,x≥0.aa0算术平方根的表示方法:a的算术平方根记为,读作“根号a”或“二次根号a”,其中a叫做被开方数.规定:0的算术平方根是0,记作.知识梳理知识回顾问题探究课堂小结随堂检测算术平方根的概念:一般地,如果一个正数x的平方为a,即x...