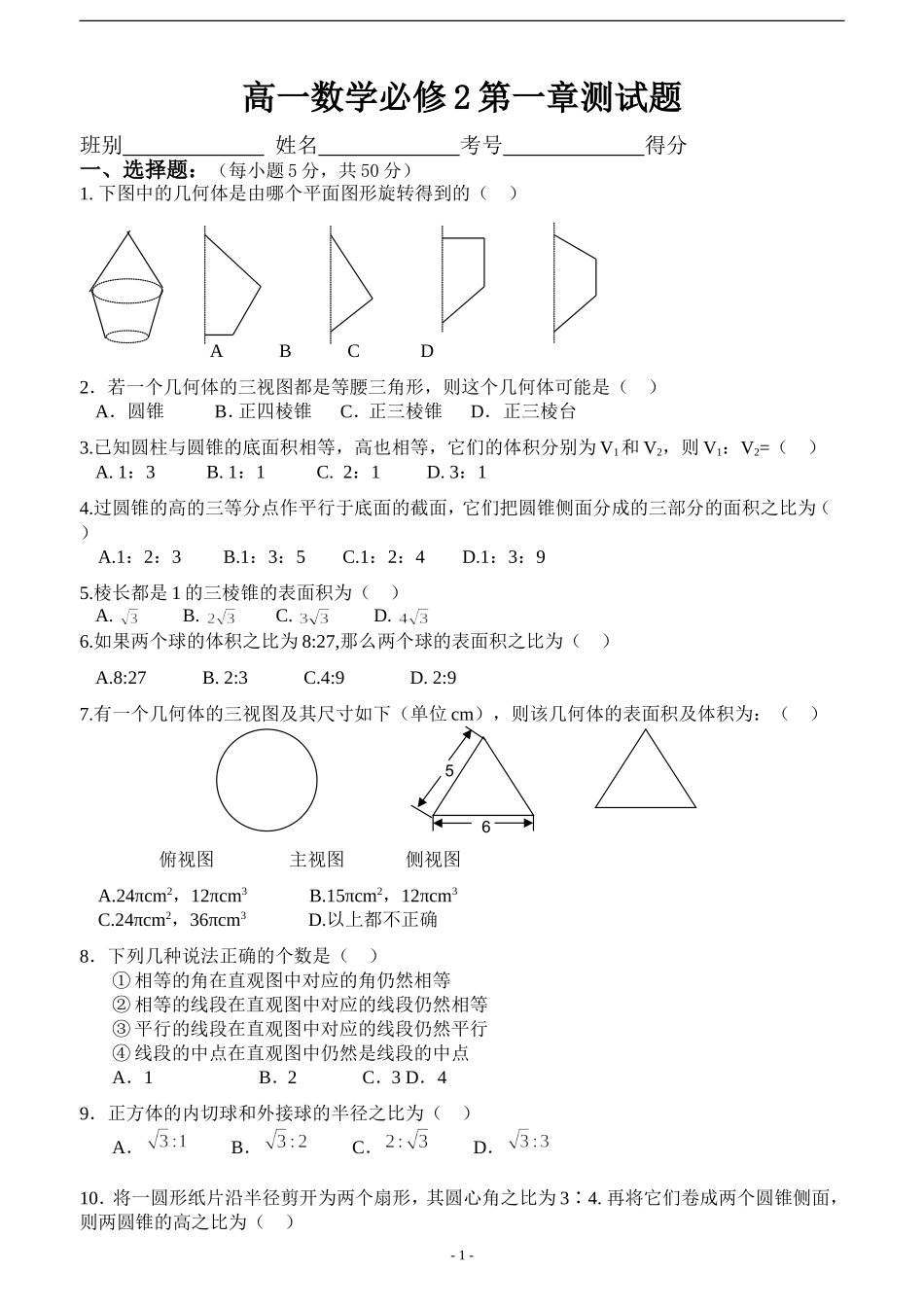
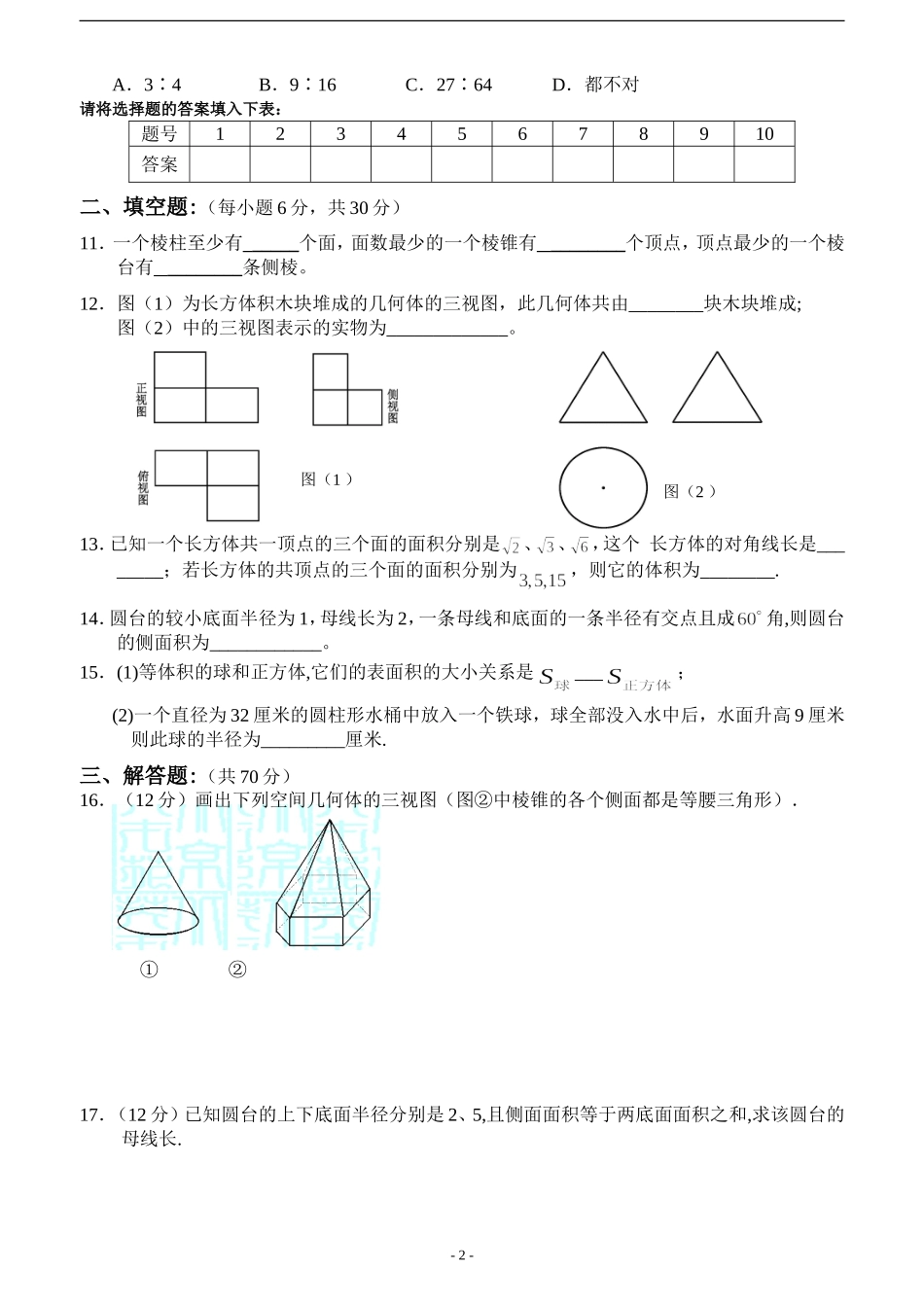
高一数学必修2第一章测试题班别姓名考号得分一、选择题:(每小题5分,共50分)1.下图中的几何体是由哪个平面图形旋转得到的()ABCD2.若一个几何体的三视图都是等腰三角形,则这个几何体可能是()A.圆锥B.正四棱锥C.正三棱锥D.正三棱台3.已知圆柱与圆锥的底面积相等,高也相等,它们的体积分别为V1和V2,则V1:V2=()A.1:3B.1:1C.2:1D.3:14.过圆锥的高的三等分点作平行于底面的截面,它们把圆锥侧面分成的三部分的面积之比为()A.1:2:3B.1:3:5C.1:2:4D.1:3:95.棱长都是1的三棱锥的表面积为()A.B.C.D.6.如果两个球的体积之比为8:27,那么两个球的表面积之比为()A.8:27B.2:3C.4:9D.2:97.有一个几何体的三视图及其尺寸如下(单位cm),则该几何体的表面积及体积为:()俯视图主视图侧视图A.24πcm2,12πcm3B.15πcm2,12πcm3C.24πcm2,36πcm3D.以上都不正确8.下列几种说法正确的个数是()①相等的角在直观图中对应的角仍然相等②相等的线段在直观图中对应的线段仍然相等③平行的线段在直观图中对应的线段仍然平行④线段的中点在直观图中仍然是线段的中点A.1B.2C.3D.49.正方体的内切球和外接球的半径之比为()A.B.C.D.10.将一圆形纸片沿半径剪开为两个扇形,其圆心角之比为3∶4.再将它们卷成两个圆锥侧面,则两圆锥的高之比为()-1-65A.3∶4B.9∶16C.27∶64D.都不对请将选择题的答案填入下表:题号12345678910答案二、填空题:(每小题6分,共30分)11.一个棱柱至少有_____个面,面数最少的一个棱锥有________个顶点,顶点最少的一个棱台有________条侧棱。12.图(1)为长方体积木块堆成的几何体的三视图,此几何体共由________块木块堆成;图(2)中的三视图表示的实物为_____________。13.已知一个长方体共一顶点的三个面的面积分别是、、,这个长方体的对角线长是________;若长方体的共顶点的三个面的面积分别为,则它的体积为________.14.圆台的较小底面半径为1,母线长为2,一条母线和底面的一条半径有交点且成角,则圆台的侧面积为____________。15.(1)等体积的球和正方体,它们的表面积的大小关系是___;(2)一个直径为32厘米的圆柱形水桶中放入一个铁球,球全部没入水中后,水面升高9厘米则此球的半径为_________厘米.三、解答题:(共70分)16.(12分)画出下列空间几何体的三视图(图②中棱锥的各个侧面都是等腰三角形).①②17.(12分)已知圆台的上下底面半径分别是2、5,且侧面面积等于两底面面积之和,求该圆台的母线长.-2-图(1)图(2)18.(14分)(如图)在底半径为,母线长为的圆锥中内接一个高为的圆柱,求圆柱的表面积.19.(16分)养路处建造圆锥形仓库用于贮藏食盐(供融化高速公路上的积雪之用),已建的仓库的底面直径为,高,养路处拟建一个更大的圆锥形仓库,以存放更多食盐,现有两种方案:一是新建的仓库的底面直径比原来大(高不变);二是高度增加(底面直径不变)。(1)分别计算按这两种方案所建的仓库的体积;(2)分别计算按这两种方案所建的仓库的表面积;(3)哪个方案更经济些?-3-20.(16分)根据给出的空间几何体的三视图,用斜二测画法画出它的直观图.(写出画法,并保留作图痕迹)正视图侧视图俯视图高一数学必修2第一章测试题(答案)一、选择题:(每小题5分,共50分)1.A2.C3.D4.B5.A6.C7.A8.B9.D10.D-4-二、填空题:(每小题6分,共30分)11.5,4,3.符合条件的几何体分别是:三棱柱,三棱锥,三棱台12.(1)4(2)圆锥13.,14.画出圆台,则15.(1)设(2)三、解答题:(共70分)16.(12分)略17.(12分)解:18.(14分)解:圆锥的高,圆柱的底面半径,19.(16分)解:(1)如果按方案一,仓库的底面直径变成,则仓库的体积如果按方案二,仓库的高变成,则仓库的体积(2)如果按方案一,仓库的底面直径变成,半径为.棱锥的母线长为则仓库的表面积如果按方案二,仓库的高变成.棱锥的母线长为则仓库的表面积-5-(3),20.(16分)解:由几何体的三视图知道,这个几何体是一个上面小而底面大的圆台,我们可以先画出上、下底面圆,再画母线.画法:(1)画轴如下图,画x轴、y轴、z轴,三轴相交于...