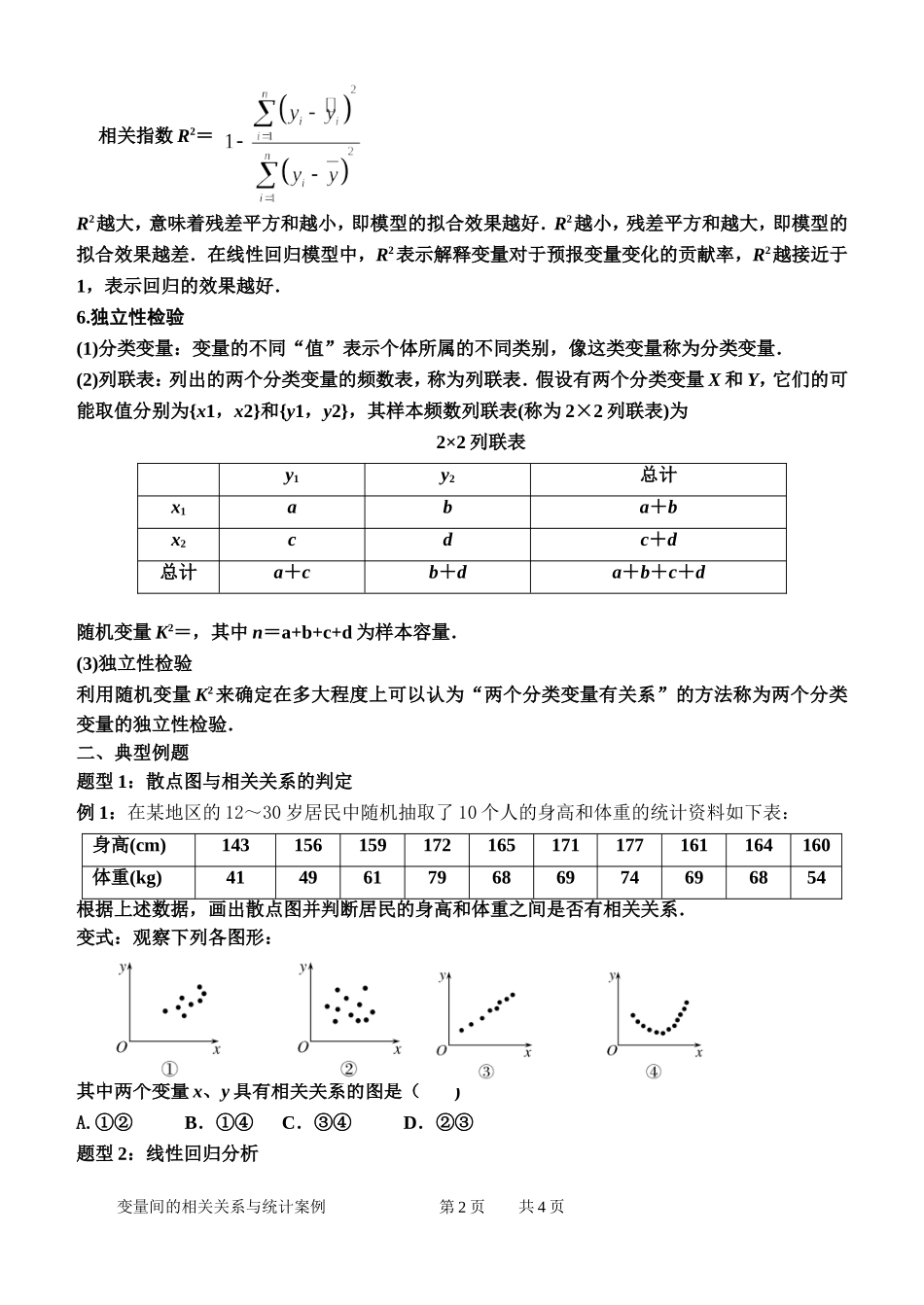
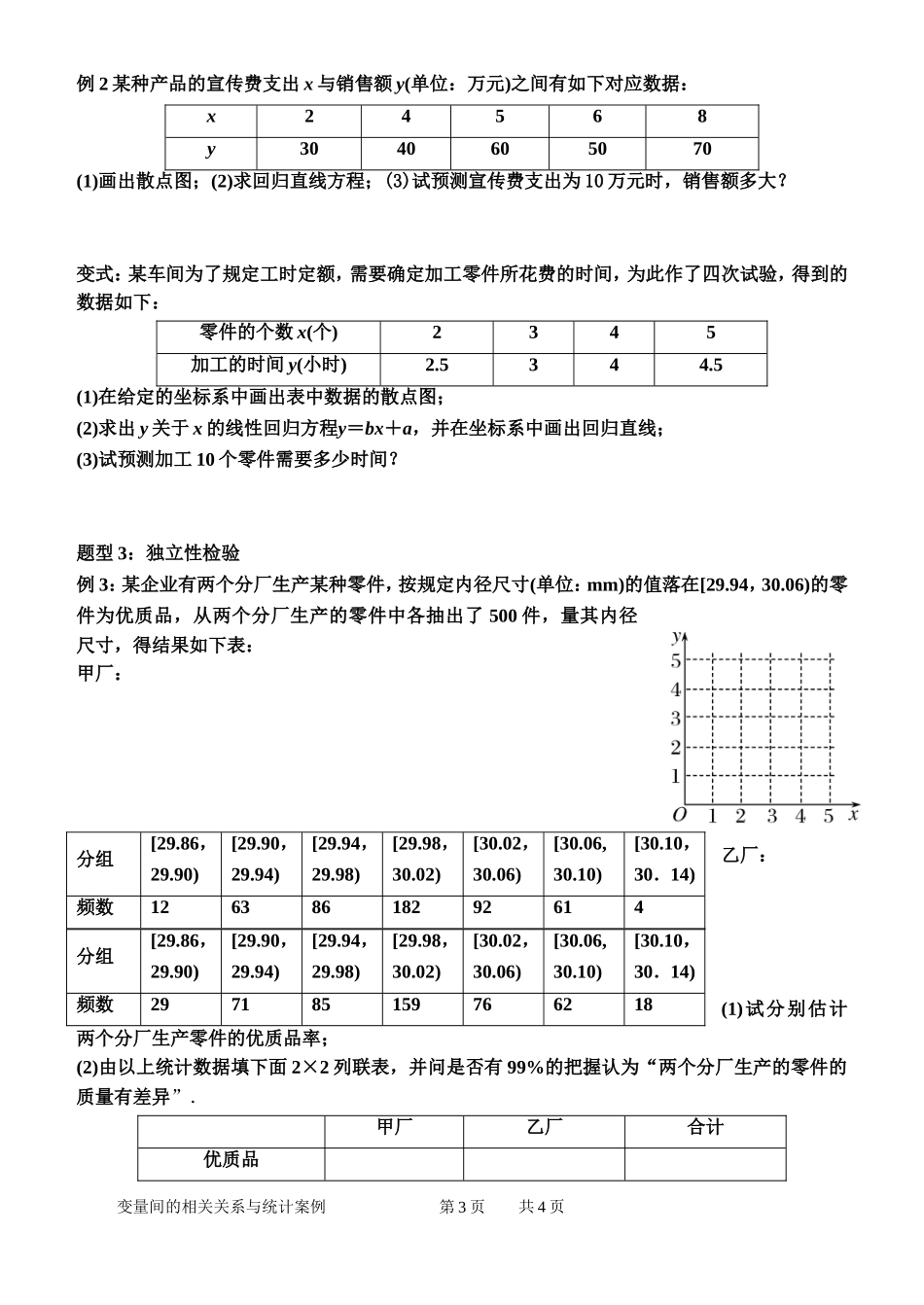
哈三中2014届高三第一轮复习变量间的相关关系与统计案例一、知识点1.两个变量的相关关系:正相关:点散布在从左下角到右上角的区域负相关:点散布在从左上角到右下角的区域2.线性相关关系与回归直线如果散点图中点的分布从整体上看大致在一条直线附近,就称这两个变量之间具有线性相关关系.这条直线叫做回归直线.3.回归直线方程与最小二乘法①n个观测值的n个点大致分布在一条直线的附近,若所求的直线方程为则我们将这个方程叫做回归直线方程,a、b叫做回归系数,相应的直线叫做回归直线.②最小二乘法使总体偏差Q=((y1-bx1-a)2+(y2-bx2-a)2+…+y(yn-bxn-a)21为最小的方法,叫最小二乘法.4.回归分析具有线性相关关系的数据(x1,y1),(x2,y2),…,(xn,yn)中,回归方程的斜率和截距的最小二乘估计分别为:其中,称为样本点的中心,线性回归方程为ya.5.残差分析(1)残差:对于样本点(x1,y1),(x2,y2),…,(xn,yn),它们的随机误差为ei=yi-bxi-a,i=1,2,…,n,其估计值为ei=yi-yi=yi-bxi-a,i=1,2,…,n,ei称为相应于点(xi,yi)的残差.(2)残差平方和变量间的相关关系与统计案例共4页第1页(3)相关指数R2=1R2越大,意味着残差平方和越小,即模型的拟合效果越好.R2越小,残差平方和越大,即模型的拟合效果越差.在线性回归模型中,R2表示解释变量对于预报变量变化的贡献率,R2越接近于1,表示回归的效果越好.6.独立性检验(1)分类变量:变量的不同“值”表示个体所属的不同类别,像这类变量称为分类变量.(2)列联表:列出的两个分类变量的频数表,称为列联表.假设有两个分类变量X和Y,它们的可能取值分别为{x1,x2}和{y1,y2},其样本频数列联表(称为2×2列联表)为2×2列联表y1y2总计x1aba+bx2cdc+d总计a+cb+da+b+c+d随机变量K2=,其中n=a+b+c+d为样本容量.(3)独立性检验利用随机变量K2来确定在多大程度上可以认为“两个分类变量有关系”的方法称为两个分类变量的独立性检验.二、典型例题题型1:散点图与相关关系的判定例1:在某地区的12~30岁居民中随机抽取了10个人的身高和体重的统计资料如下表:身高(cm)143156159172165171177161164160体重(kg)41496179686974696854根据上述数据,画出散点图并判断居民的身高和体重之间是否有相关关系.变式:观察下列各图形:其中两个变量x、y具有相关关系的图是()A.①②B.①④C.③④D.②③题型2:线性回归分析变量间的相关关系与统计案例共4页第2页例2某种产品的宣传费支出x与销售额y(单位:万元)之间有如下对应数据:x24568y3040605070(1)画出散点图;(2)求回归直线方程;(3)试预测宣传费支出为10万元时,销售额多大?变式:某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:零件的个数x(个)2345加工的时间y(小时)2.5344.5(1)在给定的坐标系中画出表中数据的散点图;(2)求出y关于x的线性回归方程y=bx+a,并在坐标系中画出回归直线;(3)试预测加工10个零件需要多少时间?题型3:独立性检验例3:某企业有两个分厂生产某种零件,按规定内径尺寸(单位:mm)的值落在[29.94,30.06)的零件为优质品,从两个分厂生产的零件中各抽出了500件,量其内径尺寸,得结果如下表:甲厂:乙厂:(1)试分别估计两个分厂生产零件的优质品率;(2)由以上统计数据填下面2×2列联表,并问是否有99%的把握认为“两个分厂生产的零件的质量有差异”.甲厂乙厂合计优质品变量间的相关关系与统计案例共4页分组[29.86,29.90)[29.90,29.94)[29.94,29.98)[29.98,30.02)[30.02,30.06)[30.06,30.10)[30.10,30.14)频数12638618292614分组[29.86,29.90)[29.90,29.94)[29.94,29.98)[29.98,30.02)[30.02,30.06)[30.06,30.10)[30.10,30.14)频数297185159766218第3页非优质品合计附:χ2=,变式:通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表:男女总计爱好402060不爱好203050总计6050110由K2=算得,K2==7.8.附表P(K2≥k)0.0500.0100.001k3.8416.63510.828参照附表,得到的正确结论是()A.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”B.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”C.有99%以上的把握认为“爱好该项运动与性别有关”D.有99%以上的把握认为“爱好该项运动与性别无关”变量间的相关关系与统计案例共4页第4页