弧长和扇形的面积钱鸣VIP免费

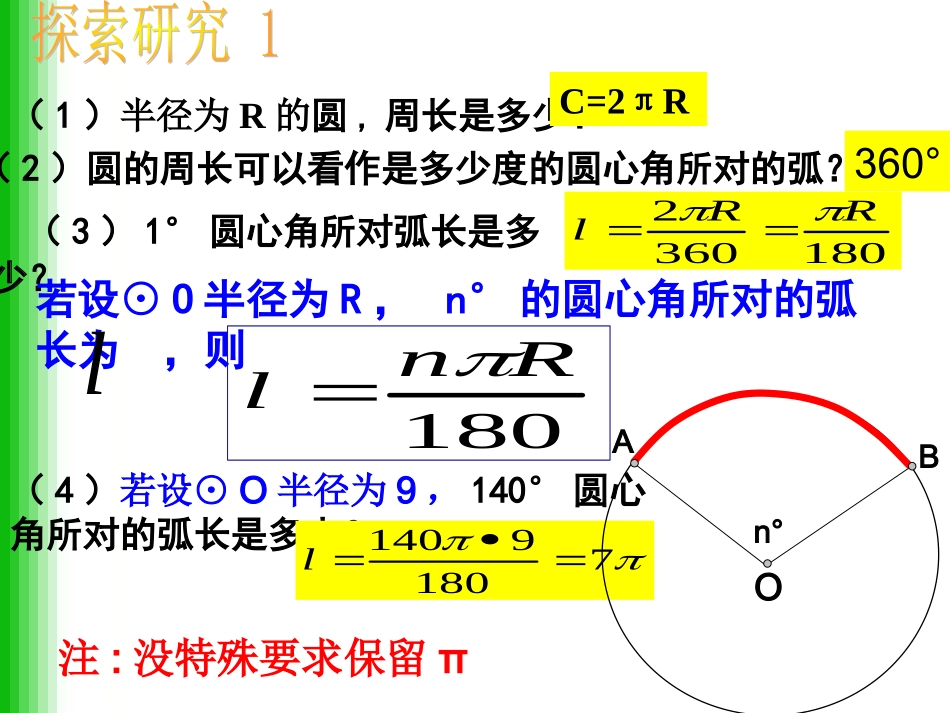
海南中学钱鸣1、本节内容主要哪些知识点？2、两个公式如何推导？（1）半径为R的圆,周长是多少？C=2πR（3）1°圆心角所对弧长是多少？（4）若设⊙O半径为9，140°圆心角所对的弧长是多少？71809140l（2）圆的周长可以看作是多少度的圆心角所对的弧？180Rnln°ABO若设⊙O半径为R，n°的圆心角所对的弧长为，则l1803602RRl360°注:没特殊要求保留π如下图，由组成圆心角的两条半径和圆心角所对的弧围成的图形是扇形。半径半径圆心角圆心角弧ABOBA扇形那么：在半径为R的圆中,n°的圆心角所对的扇形面积的计算公式为360Rn2扇形S如果圆的半径为R，则圆的面积为，l°的圆心角对应的扇形面积为，°的圆心角对应的扇形面积为2R3602Rn36036022RnRnn°lO比较扇形面积(S)公式和弧长(l)公式,你能用弧长来表示扇形的面积吗?12SRl探索弧长与扇形面积的关系SR想一想：扇形的面积公式与什么公式类似？3602RnS扇形180RnlABOO比较扇形面积与弧长公式,用弧长表示扇形面积:lRS21扇形1个圆面积21个圆面积41个圆面积43个圆面积1、举例说明怎样应用这两个图形公式进行有关计算？2、运用这两个公式有何注意点？练习：1.如图、水平放置的圆柱形排水管道的截面半径是0.6cm，其中水面高0.9cm，求截面上有水部分的面积。(结果保留)0ABDCE有水部分的面积=S扇+S△309.024.0变式：如图、水平放置的圆柱形排水管道的截面半径是0.6cm，其中水面高0.3cm，求截面上有水部分的面积。（精确到0.01cm）。0BACD弓形的面积=S扇-S⊿4、如图所示，分别以n边形的顶点为圆心，以单位1为半径画圆，则图中阴影部分的面积之和为个平方单位．再见