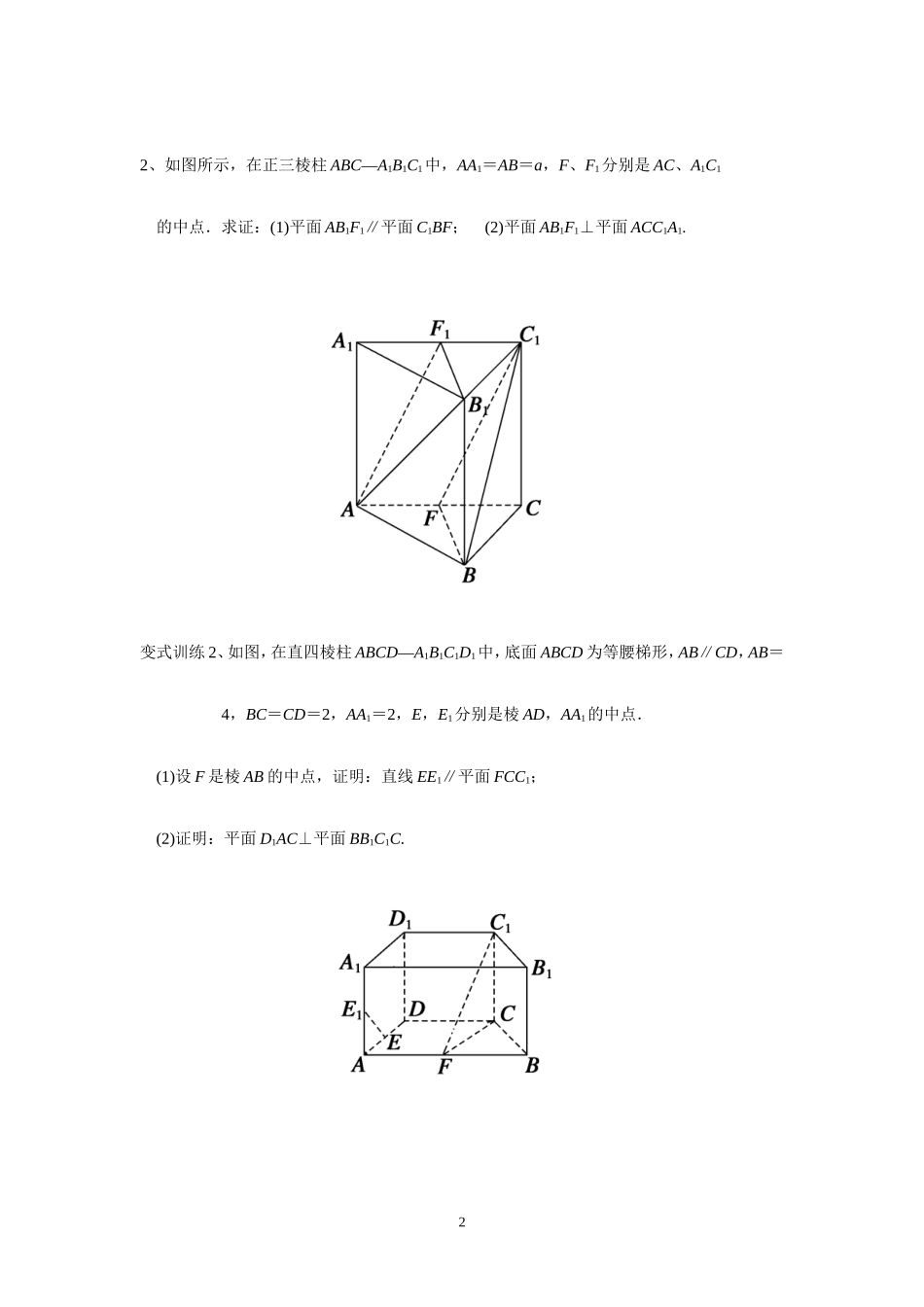
立体几何训练1、如图所示,正三棱柱A1B1C1—ABC中,点D是BC的中点,BC=BB1,设B1D∩BC1=F.求证:(1)A1C∥平面AB1D;(2)BC1⊥平面AB1D.变式训练1、如图所示,在四棱锥P—ABCD中,PD⊥平面ABCD,AD⊥CD,DB平分∠ADC,E为PC的中点,AD=CD.求证:(1)PA∥平面BDE;(2)AC⊥平面PBD.12、如图所示,在正三棱柱ABC—A1B1C1中,AA1=AB=a,F、F1分别是AC、A1C1的中点.求证:(1)平面AB1F1∥平面C1BF;(2)平面AB1F1⊥平面ACC1A1.变式训练2、如图,在直四棱柱ABCD—A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E,E1分别是棱AD,AA1的中点.(1)设F是棱AB的中点,证明:直线EE1∥平面FCC1;(2)证明:平面D1AC⊥平面BB1C1C.23、如图,平行四边形ABCD中,∠DAB=60°,AB=2,AD=4.将△CBD沿BD折起到△EBD的位置,使平面EBD⊥平面ABD.(1)求证:AB⊥DE.(2)求三棱锥E—ABD的侧面积.变式训练3、如下图(1)所示,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD=2.E,F,G分别为线段PC,PD,BC的中点,现将△PDC折起,使平面PDC⊥平面ABCD(图(2)).(1)求证:AP∥平面EFG;(2)在线段PB上确定一点Q,使PC⊥平面ADQ,试给出证明.3