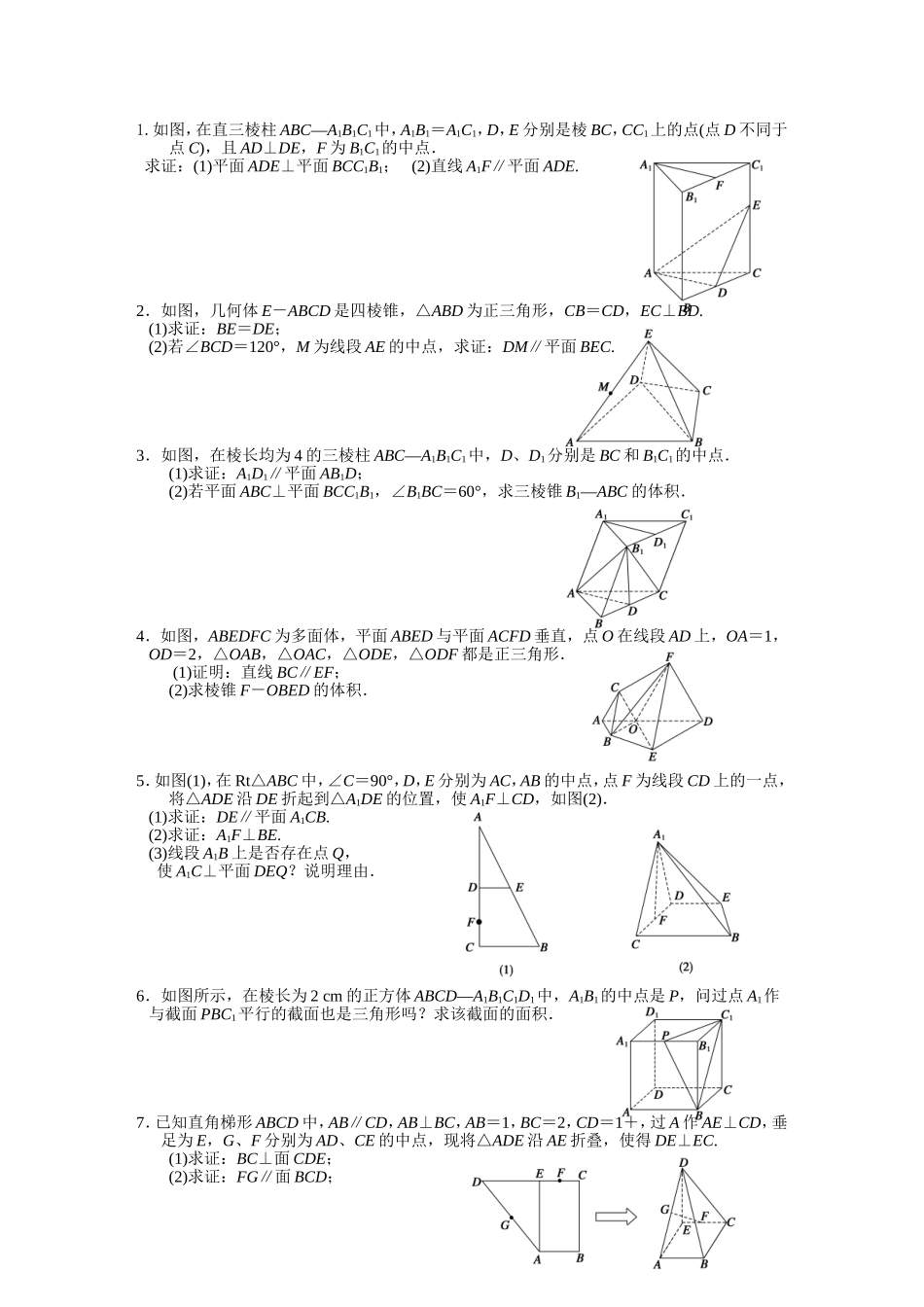
1.如图,在直三棱柱ABC—A1B1C1中,A1B1=A1C1,D,E分别是棱BC,CC1上的点(点D不同于点C),且AD⊥DE,F为B1C1的中点.求证:(1)平面ADE⊥平面BCC1B1;(2)直线A1F∥平面ADE.2.如图,几何体E-ABCD是四棱锥,△ABD为正三角形,CB=CD,EC⊥BD.(1)求证:BE=DE;(2)若∠BCD=120°,M为线段AE的中点,求证:DM∥平面BEC.3.如图,在棱长均为4的三棱柱ABC—A1B1C1中,D、D1分别是BC和B1C1的中点.(1)求证:A1D1∥平面AB1D;(2)若平面ABC⊥平面BCC1B1,∠B1BC=60°,求三棱锥B1—ABC的体积.4.如图,ABEDFC为多面体,平面ABED与平面ACFD垂直,点O在线段AD上,OA=1,OD=2,△OAB,△OAC,△ODE,△ODF都是正三角形.(1)证明:直线BC∥EF;(2)求棱锥F-OBED的体积.5.如图(1),在Rt△ABC中,∠C=90°,D,E分别为AC,AB的中点,点F为线段CD上的一点,将△ADE沿DE折起到△A1DE的位置,使A1F⊥CD,如图(2).(1)求证:DE∥平面A1CB.(2)求证:A1F⊥BE.(3)线段A1B上是否存在点Q,使A1C⊥平面DEQ?说明理由.6.如图所示,在棱长为2cm的正方体ABCD—A1B1C1D1中,A1B1的中点是P,问过点A1作与截面PBC1平行的截面也是三角形吗?求该截面的面积.7.已知直角梯形ABCD中,AB∥CD,AB⊥BC,AB=1,BC=2,CD=1+,过A作AE⊥CD,垂足为E,G、F分别为AD、CE的中点,现将△ADE沿AE折叠,使得DE⊥EC.(1)求证:BC⊥面CDE;(2)求证:FG∥面BCD;(3)在线段AE上找一点R,使得面BDR⊥面DCB,并说明理由.8.如图,PA垂直于矩形ABCD所在的平面,M、N分别是AB、PC的中点,∠PDA=45°,(1)求证:MN⊥平面PCD.(2)试问矩形ABCD满足什么条件时,PC⊥BD.9.如图,四边形ABCD为正方形,QA⊥平面ABCD,PD∥QA,QA=AB=PD.(1)证明:PQ⊥平面DCQ;(2)求棱锥Q-ABCD的体积与棱锥P-DCQ的体积的比值.10.如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB=AD,∠BAD=60°,E,F分别是AP,AD的中点.求证:(1)直线EF∥平面PCD;(2)平面BEF⊥平面PAD.11.已知等腰梯形PDCB中,PB=3,DC=1,PD=BC=,A为PB边上一点,且DA⊥PB,现将△PAD沿AD折起,使面PAD⊥面ABCD(如图所示).(1)证明:平面PAD⊥平面PCD;(2)试在棱PB上确定一点M,使截面AMC把几何体分成两部分VP—DCMA∶VM—ACB=2∶1;(3)在M点满足(2)的情况下,判断直线PD是否平行于平面AMC,并说明理由.12.如图,在多面体ABCDEF中,四边形ABCD是正方形,EF∥AB,EF⊥FB,AB=2EF,∠BFC=90°,BF=FC,H为BC的中点.(1)求证:FH∥平面EDB;(2)求证:AC⊥平面EDB.