离散型随机变量的均值(数学期望1)443VIP免费

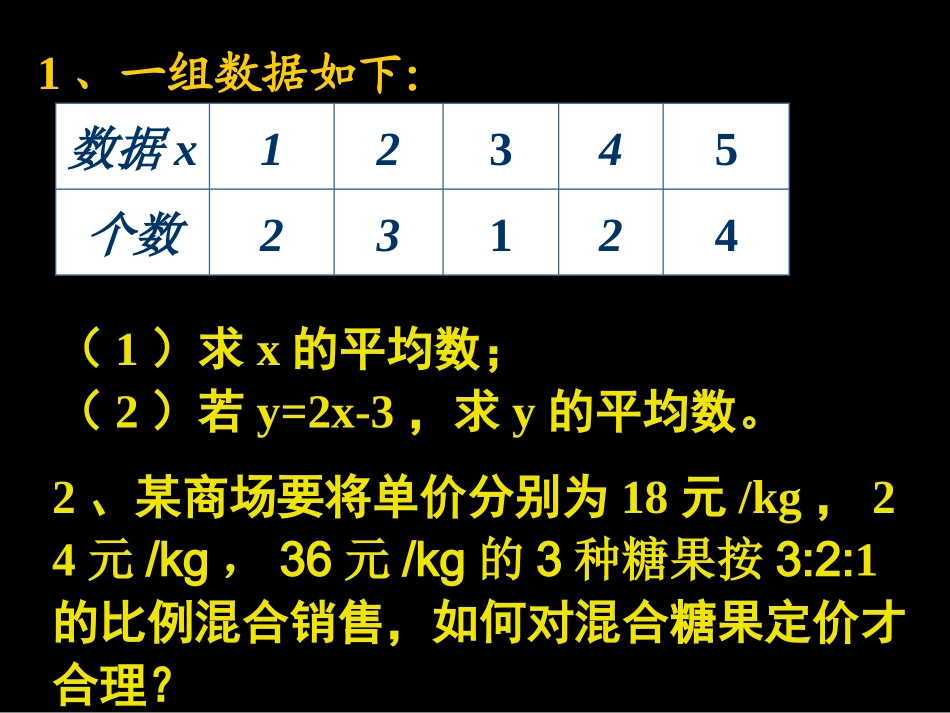
离散型随机变量的均值(数学期望1)研读教材P60-P61:1.回顾加权平均数的公式；2.加权平均数与离散型随机变量的分布列有怎样的关系;3.如何理解随机变量X的均值(数学期望)?4.教材P62思考:“随机变量的均值与样本的平均值有何联系与区别？”1、一组数据如下：数据x12345个数23124（1）求x的平均数；（2）若y=2x-3，求y的平均数。2、某商场要将单价分别为18元/kg，24元/kg，36元/kg的3种糖果按3:2:1的比例混合销售，如何对混合糖果定价才合理？随机变量X的均值(数学期望):一般地,若离散型随机变量X的分布列为:Xx1x2……xi……xnPp1p2……pi……pn则E(X)=x1p1+x2p2+……+xnpn为随机变量X的均值(数学期望)如：抛掷一枚骰子，所得点数X的期望为（）A.0.6B.1C.3.5D.2探究1.已知随机变量X的数学期望为E(X),若Y=aX+b,其中a、b为常数,则Y也是随机变量,则E(Y)=E(aX+b)=aE(X)+b探究2.①若随机变量X服从二点分布,那么E(X)=P;②若X~B(n,p),则E(X)=nP.例1.在篮球比赛中,罚球命中1次得1分,不中得0分,某运动员罚球命中率为0.7,(1)求他罚球1次的得分X的均值；(2)若重复5次罚球，求命中次数Y的均值。2.抛掷一枚硬币、规定正面向上得1分，反面向上得-1分，求得分X的均值。1.已知随机变量X的分布列为：求E(X)X012345P0.10.20.30.20.10.1练习：例2.已知随机变量X的分布列如下：（1）求m的值；（2）求E(X);（3）若Y=2X+0.3，求E(aY).（4）若Y=aX+2，且E(Y)=1.4，求a的值。X-2-1012P0.250.20.1m0.1例3.一次单元测验由20个选择题构成,每个选择题有4个选项,其中仅有一个选项正确,每题对得5分,不选或选错不得分,满分100分。学生甲选对任意一题的概率为0.9,学生乙则在测验中对每题都从各选项中随机地选择一个,分别求学生甲与乙在这次测验中的成绩的均值。求随机变量X的均值(数学期望)的一般方法：法一：随机变量X的分布列；法二：利用两个重要结论：①E(aX+b)=aE(X)+b(a、b为常数);②若X~B(n,p),则E(X)=nPP64练习5、同时抛掷5枚质地均匀的硬币，求出现正面向上的硬币数X的均值。1.设E（X）=10，则E（3X－5）=____2.若随机变量X～B（n，0.6），且E（X)=3，则P（X=1）=（）A.2×0.44B.2×0.44C.3×0.44D.3×0.643.设随机变量X的分布列为:则E（X）=_______)300,,1,0()32()31()(300300kCkXPkkk预习：教材P68-P69：作业：活页训练P113-114