卡诺图化简法VIP免费

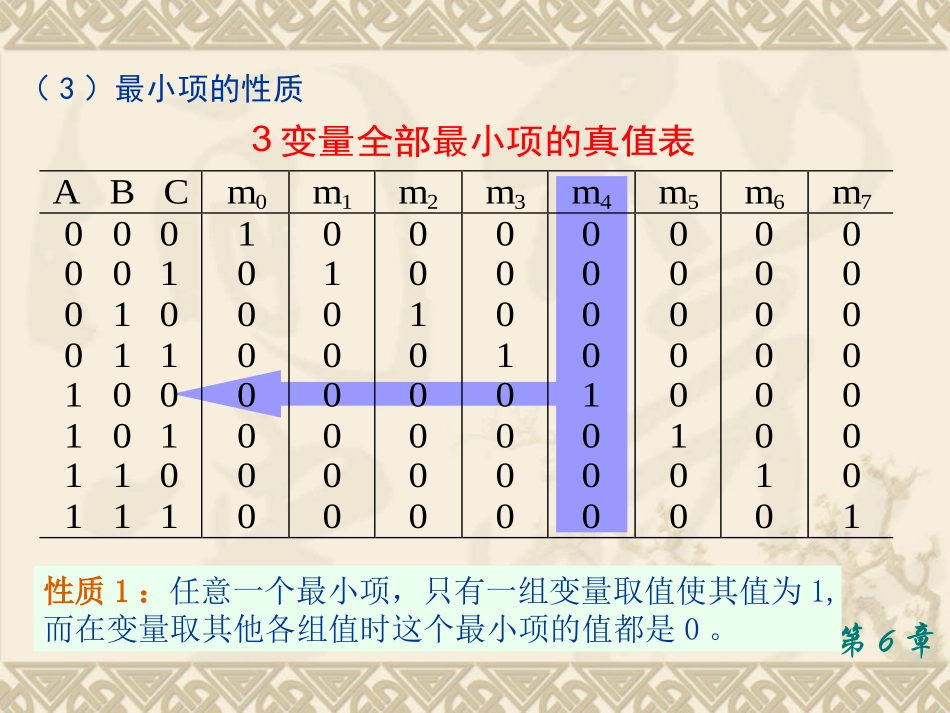
五．逻辑函数的卡诺图化简法1.关于“最小项”第6章返回（1）最小项定义如果一个函数的某个乘积项包含了函数的全部变量，其中每个变量都以原变量或反变量的形式出现，且仅出现一次，则这个乘积项称为该函数的一个标准积项，通常称为最小项。3个变量A、B、C可组成8个最小项：ABCCABCBACBABCACBACBACBA、、、、、、、（2）最小项的表示方法通常用符号mi来表示最小项。下标i的确定：把最小项中的原变量记为1，反变量记为0，当变量顺序确定后，可以按顺序排列成一个二进制数，则与这个二进制数相对应的十进制数，就是这个最小项的下标i。3个变量A、B、C的8个最小项可以分别表示为：ABCmCABmCBAmCBAmBCAmCBAmCBAmCBAm76543210、、、、、、第6章（3）最小项的性质性质1：任意一个最小项，只有一组变量取值使其值为1,而在变量取其他各组值时这个最小项的值都是0。第6章3变量全部最小项的真值表ABCm0m1m2m3m4m5m6m70000010100111001011101111000000001000000001000000001000000001000000001000000001000000001（3）最小项的性质性质2：不同的最小项，使它的值为1的那一组变量取值也不同。第6章3变量全部最小项的真值表ABCm0m1m2m3m4m5m6m70000010100111001011101111000000001000000001000000001000000001000000001000000001000000001（3）最小项的性质3变量全部最小项的真值表ABCm0m1m2m3m4m5m6m70000010100111001011101111000000001000000001000000001000000001000000001000000001000000001性质3：任意两个不同的最小项的乘积必为0。第6章ABCABC0CB0CBAACBACBA（3）最小项的性质性质4：全部最小项的和必为1。第6章3变量全部最小项的真值表ABCm0m1m2m3m4m5m6m70000010100111001011101111000000001000000001000000001000000001000000001000000001000000001变量ABC取值为001情况下，各最小项之和为1。【因为其中只有一个最小项为1，其余全为0。】任何一个逻辑函数都可以表示成唯一的一组最小项之和，称为标准与或表达式，也称为最小项表达式。对于不是最小项表达式的与或表达式，可利用公式A＋A＝1和A(B+C)＝AB＋BC来配项展开成最小项表达式。第6章（4）逻辑函数的最小项表达式例如：C)BB(A)CC(ABCAAB)C,B,A(L【表示法1】CBABCACABABC【表示法2】1367mmmm【表示法3】7,6,3,1m【表示法4】ii)7,6,3,1i(m【表示法5】)7,6,3,1(最小项的若干表示方法第6章BCAY第6章例：将下列函数化为最小项之和的形式BC)AA()CC)(BB(ABCAABCCBACBACBABCAABCBCACBACBACBA73210mmmmm)7,3,2,1,0(m添项第6章如果列出了函数的真值表，则只要将函数值为1的那些最小项相加，便是函数的最小项表达式。CBAm1CBAm2BCAm3已知真值表，写出函数的最小项之和的形式CBAm5CBACBACBACBA)5,3,2,1(mmmmmY5321将真值表中函数值为0的那些最小项相加，便可得到反函数的最小项表达式。第6章则由真值表可得如下逻辑表达式：注意：在n个变量的逻辑系统中，如果Y为i个最小项之和，则必为余下的（n－i）个最小项之和。Y（5）最小项的相邻性任何两个最小项如果他们只有一个因子不同，其余因子都相同，则称这两个最小项为相邻最小项。显然，m0与m1具有相邻性，而与不相邻，因为他们有两个因子不相同。m3与m4也不相邻，而m3与m2相邻。)CBA(m1)CBA(m2CAC)BB(ACBACBAmm20第6章相邻的两个最小项之和可以合并成一项，并消去一个变量。如：对于有对于有nn个变量的逻辑函数，其最小项有个变量的逻辑函数，其最小项有22nn个。个。因此该逻辑函数的卡诺图由因此该逻辑函数的卡诺图由22nn个小方格构成，每个小方格个小方格构成，每个小方格都满足逻辑相邻项的要求。都满足逻辑相邻项的要求。分别画出了二、三、四个变量的卡诺图。分别画出了二、三、四个变量的卡诺图。2.2.卡诺图卡诺图◆◆基本知识基本知识卡诺图是由美国工程师卡诺（卡诺图是由美国工程师卡诺（KarnaughKarnaugh）首先提出）首先提出的一种用来描述逻辑函数的特殊方格图。的一种用来描述逻辑函数的特...