高考数学复习专题八第1讲 几何证明选讲课件 理 课件VIP免费

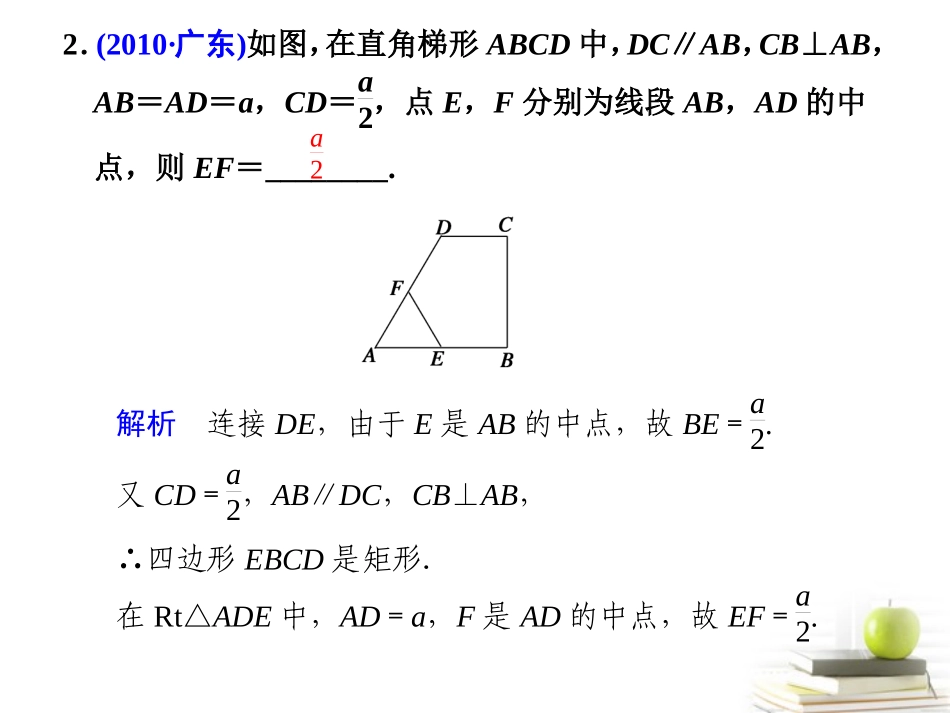
专题八系列4选讲§1几何证明选讲真题热身1．(2011·陕西)如图，∠B＝∠D，AE⊥BC，∠ACD＝90°，且AB＝6，AC＝4，AD＝12，则BE＝________.解析 AC＝4，AD＝12，∠ACD＝90°，∴CD2＝AD2－AC2＝128，∴CD＝82.又 AE⊥BC，∠B＝∠D，∴△ABE∽△ADC，∴ABAD＝BEDC，∴BE＝AB·DCAD＝6×8212＝42.422．(2010·广东)如图，在直角梯形ABCD中，DC∥AB，CB⊥AB，AB＝AD＝a，CD＝a2，点E，F分别为线段AB，AD的中点，则EF＝________.解析连接DE，由于E是AB的中点，故BE＝a2.又CD＝a2，AB∥DC，CB⊥AB，∴四边形EBCD是矩形．在Rt△ADE中，AD＝a，F是AD的中点，故EF＝a2.a2考点整合1．平行线等分线段定理：如果一组平行线在一条直线上截得的线段相等，那么在其他直线上截得的线段也相等．2．平行截割定理(平行线分线段成比例定理)三条平行线截两条直线，所得的对应线段成比例．3．相似三角形的判定定理判定定理1：对于任意两个三角形，如果一个三角形的两个角与另一个三角形的两个角对应相等，那么这两个三角形相似．判定定理2：如果一个三角形的两边和另一个三角形的两边对应成比例，并且夹角相等，那么这两个三角形相似．判定定理3：对于任意两个三角形，如果一个三角形的三条边和另一个三角形的三条边对应成比例，那么这两个三角形相似．4．相似三角形的性质(1)相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比；(2)相似三角形周长的比等于相似比；(3)相似三角形面积的比等于相似比的平方．5．直角三角形的射影定理：直角三角形中，每一条直角边是这条直角边在斜边上的射影和斜边的比例中项；斜边上的高是两条直角边在斜边上的射影的比例中项．6．圆周角定理圆上一条弧所对的圆周角等于它所对的圆心角的一半．7．圆心角定理：圆心角的度数等于它所对弧的度数．8．圆内接四边形的性质定理：(1)圆的内接四边形的对角互补．(2)圆内接四边形的外角等于它的内角的对角．9．圆内接四边形判定定理：如果一个四边形的对角互补，那么这个四边形的四个顶点共圆．10．圆的切线的判定定理：经过半径的外端并且垂直于这条半径的直线是圆的切线．11．切线的性质定理：圆的切线垂直于经过切点的半径．12．弦切角定理：弦切角等于它所夹的弧所对的圆周角．13．相交弦定理：圆内的两条相交弦，被交点分成的两条线段长的积相等．14．切割线定理：从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比例中项．分类突破一、相似三角形与比例线段例1如图，AE∥BF∥CG∥DH，AB＝12BC＝CD，AE＝12，DH＝16，AH交BF于M，则BM＝______，CG＝______.解析 AE∥BF∥CG∥DH，AB＝12BC＝CD，AE＝12，DH＝16，∴ABAD＝14，BMDH＝ABAD.∴BM16＝14，∴BM＝4.取BC的中点P，作PQ∥DH交EH于Q，如图，则PQ是梯形ADHE的中位线，∴PQ＝12(AE＋DH)＝12(12＋16)＝14.同理：CG＝12(PQ＋DH)＝12(14＋16)＝15.答案415归纳拓展有关两线段的比值的问题，除了应用平行线分线段成比例定理外，也可利用相似三角形的判定和性质求解．解题中要注意观察图形特点，巧添辅助线，对解题可起到事半功倍的效果．变式训练1如右图，在梯形ABCD中，AB∥CD，且AB＝2CD，E、F分别是AB、BC的中点，EF与BD相交于点M.若DB＝9，则BM＝________.解析 E是AB的中点，∴AB＝2EB. AB＝2CD，∴CD＝EB.又AB∥CD，∴四边形CBED是平行四边形．∴CB∥DE，∴∠DEM＝∠BFM，∠EDM＝∠FBM，∴△EDM∽△FBM.∴DMBM＝DEBF. F是BC的中点，∴DE＝2BF.∴DM＝2BM，∴BM＝13DB＝3.3点评与圆有关的比例线段问题通常要考虑利用：①相交弦定理；②割线定理；③切割线定理；④相似三角形的判定和性质等．二、与圆有关的比例线段例2如图，PC是⊙O的切线，C为切点，PAB为割线，PC=4，PB=8，∠B=30˚，则BC=.解析连接AC， PC2=PA·PB，∴PA=2，∠ACP=∠B=30˚，在△PAC中，由正弦定理得∴sin∠PAC=1，从而∠PAC=90˚，∠P=60˚，∠PCB=90˚，,sin430sin2PAC2243.BCPBPC43变式训练2如图所示，PT为⊙O的切线，T为切点，PA是割线，它与⊙O的交点是A、B，与直径CT的交点是D，已知CD＝2，AD＝3，BD＝4，那么PB＝________....