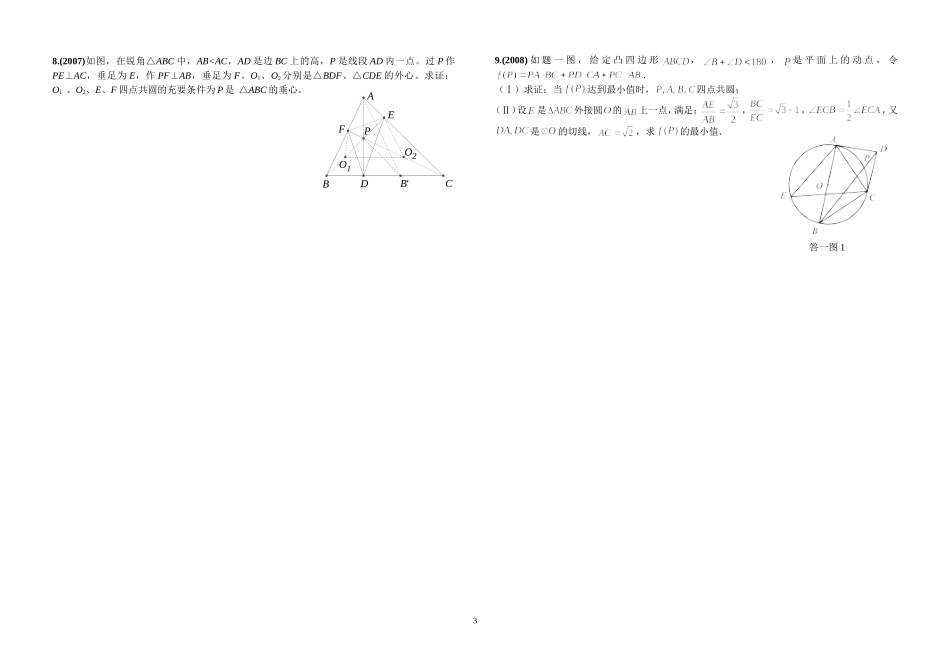
全国高中数学联赛平面几何题1.(2000)如图,在锐角三角形ABC的BC边上有两点E、F,满足∠BAE=∠CAF,作FM⊥AB,FN⊥AC(M、N是垂足),延长AE交三角形ABC的外接圆于D.证明:四边形AMDN与三角形ABC的面积相等.2.(2001)如图,△ABC中,O为外心,三条高AD、BE、CF交于点H,直线ED和AB交于点M,FD和AC交于点N.求证:(1)OB⊥DF,OC⊥DE;(2)OH⊥MN.3.(2002)4.(2003)过圆外一点P作圆的两条切线和一条割线,切点为A,B所作割线交圆于C,D两点,C在P,D之间,在弦CD上取一点Q,使∠DAQ=∠PBC.求证:∠DBQ=∠PAC.1ABCDEFMN5.(2004)在锐角三角形ABC中,AB上的高CE与AC上的高BD相交于点H,以DE为直径的圆分别交AB、AC于F、G两点,FG与AH相交于点K。已知BC=25,BD=20,BE=7,求AK的长。6.(2005)7.(2006)以B0和B1为焦点的椭圆与△AB0B1的边ABi交于点Ci(i=0,1).在AB0的延长线上任取点P0,以B0为圆心,B0P0为半径作圆弧P0Q0交C1B0的延长线于Q0;以C1为圆心,C1Q0为半径作圆弧Q0P1交B1A的延长线于点P1;以B1为圆心,B1P1为半径作圆弧P1Q1交B1C0的延长线于Q1;以C0为圆心,C0Q1为半径作圆弧Q1P0(,交AB0的延长线于P0.试证:⑴点P0与点P0重合,且圆弧P0Q0与P0Q1相内切于点P0;⑵四点P0,Q0,Q1,P1共圆.2PB1B0C1P1P0Q1Q0AC08.(2007)如图,在锐角△ABC中,AB