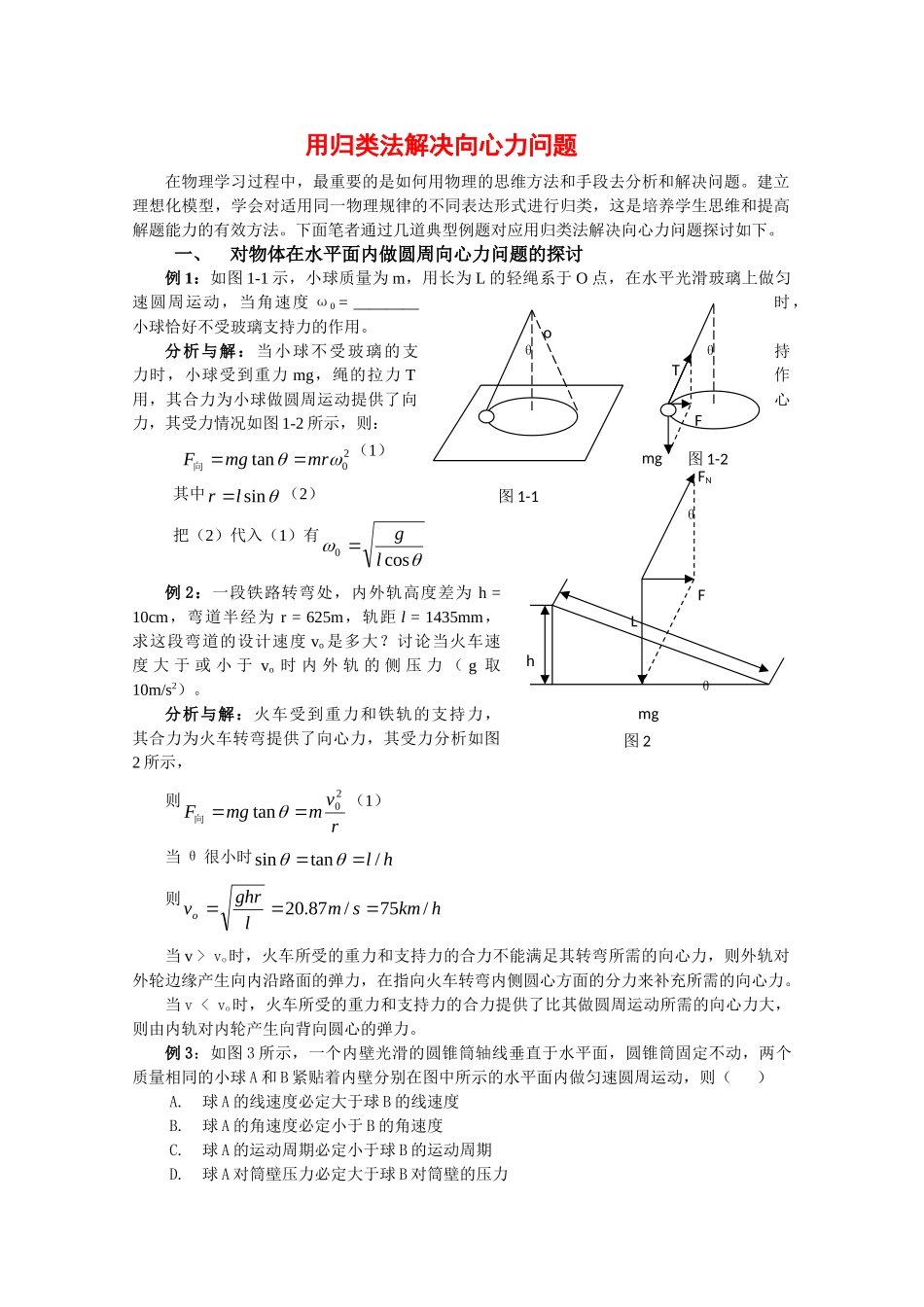
用归类法解决向心力问题在物理学习过程中,最重要的是如何用物理的思维方法和手段去分析和解决问题。建立理想化模型,学会对适用同一物理规律的不同表达形式进行归类,这是培养学生思维和提高解题能力的有效方法。下面笔者通过几道典型例题对应用归类法解决向心力问题探讨如下。一、对物体在水平面内做圆周向心力问题的探讨例1:如图1-1示,小球质量为m,用长为L的轻绳系于O点,在水平光滑玻璃上做匀速圆周运动,当角速度ω0=________时,小球恰好不受玻璃支持力的作用。分析与解:当小球不受玻璃的支持力时,小球受到重力mg,绳的拉力T作用,其合力为小球做圆周运动提供了向心力,其受力情况如图1-2所示,则:20tanmrmgF向(1)其中sinlr(2)把(2)代入(1)有cos0lg例2:一段铁路转弯处,内外轨高度差为h=10cm,弯道半经为r=625m,轨距l=1435mm,求这段弯道的设计速度vo是多大?讨论当火车速度大于或小于vo时内外轨的侧压力(g取10m/s2)。分析与解:火车受到重力和铁轨的支持力,其合力为火车转弯提供了向心力,其受力分析如图2所示,则rvmmgF20tan向(1)当θ很小时hl/tansin则hkmsmlghrvo/75/87.20当v>vo时,火车所受的重力和支持力的合力不能满足其转弯所需的向心力,则外轨对外轮边缘产生向内沿路面的弹力,在指向火车转弯内侧圆心方面的分力来补充所需的向心力。当v