正弦定理(一)课件VIP免费

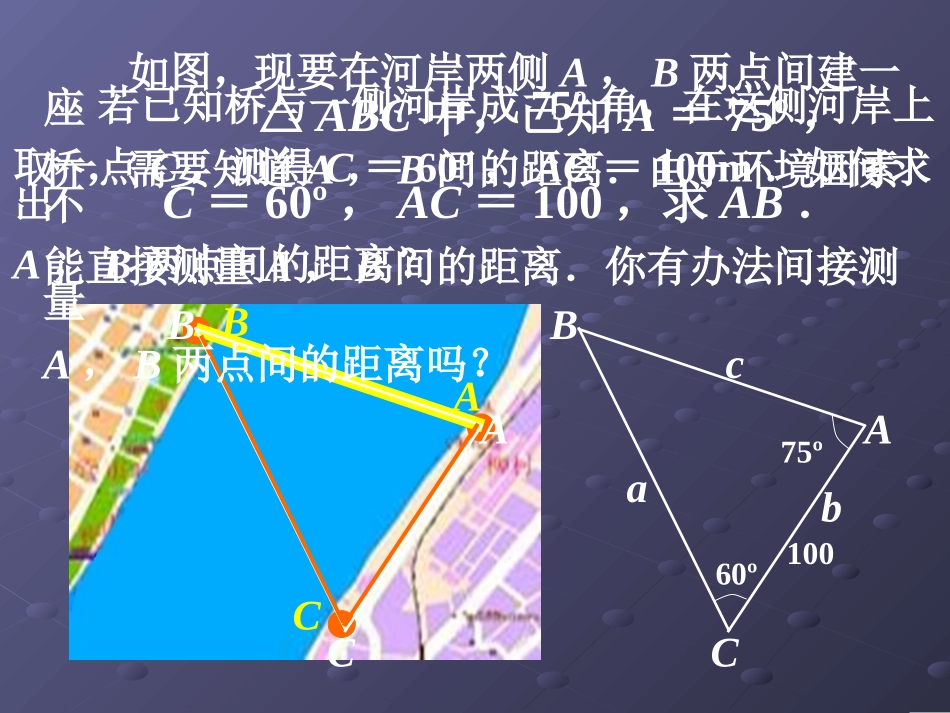
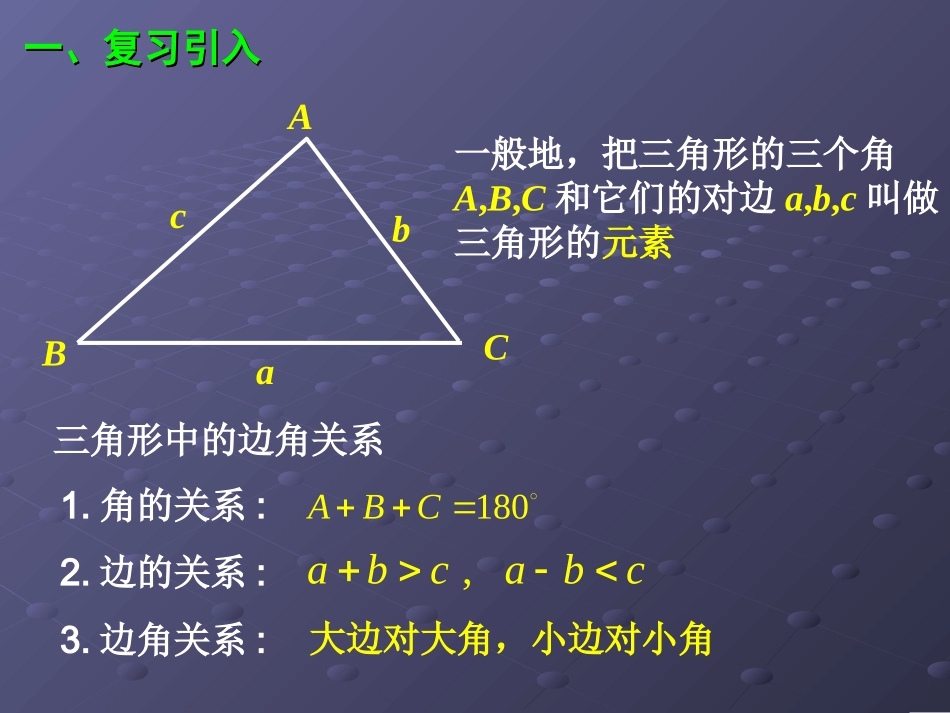
（第一课时）ABCABC如图，现要在河岸两侧A，B两点间建一座桥，需要知道A，B间的距离．由于环境因素不能直接测量A，B间的距离．你有办法间接测量A，B两点间的距离吗？若已知桥与一侧河岸成75º角，在这侧河岸上取一点C，测得C＝60º，AC＝100m．如何求出A，B两点间的距离？ABC75º60º100△ABC中，已知A＝75º，C＝60º，AC＝100，求AB．abc一、复习引入一、复习引入ABCbc三角形中的边角关系1.角的关系:2.边的关系:3.边角关系:180ABC,abcabc大边对大角，小边对小角a一般地，把三角形的三个角A,B,C和它们的对边a,b,c叫做三角形的元素直角三角形中直角三角形中::sin,sin,sin1abABCccABCabc,,sinsinsinabccccABC即sinsinsinabcABC斜三角形中这一关系式是否仍成立呢?一、复习引入一、复习引入试借助三角形的高来寻找三角形的边与角之间的关系？（1）锐角三角形：BCAabcDE（2）直角三角形：CABabc二、新课讲解二、新课讲解abcsinAsinBsinCabcsinAsinBsinC试借助三角形的高来寻找三角形的边与角之间的关系？二、新课讲解二、新课讲解（3）钝角三角形：（∠C为钝角）CABabcDE作CD垂直于AB于D，则可得sinsinCDaBbAsinsinabAB作BE垂直于AC的延长线于E，则sinsinBEcAaBCEBCECsinsin()sincAaCaCsinsinacACabcsinAsinBsinCabcsinAsinBsinC正弦定理:在一个三角形中，各边和它所对角的正弦的比相等。即:二、新课讲解二、新课讲解BCAabc定理理解(1)正弦定理说明同一三角形中，边与其对角的正弦成正比，且比例系数为同一正数，即存在正数k使；sin,sin,sinakAbkBckC(2)等价于,,从而知正弦定理的基本作用为：①已知三角形的任意两角及其一边可以求其他边，如；②已知三角形的任意两边与其中一边的对角可以求其他角的正弦值，如.sinsinsinabcABCsinsinabABsinsinbcBCsinsinacACsinsinbAaBsinsinaABb(3)其他变式：①②sin:sin:sin::ABCabcsinsinsinsinsinsinabcabcABCABC一般地，已知三角形的某些边和角，求其他的边和角的过程叫作解三角形.ABC60º75º100△ABC中，已知A＝75º，C＝60º，AC＝100，求AB．二、新课讲解二、新课讲解三、例题讲解三、例题讲解例1.在△ABC中，A=32.0º，B=81.5º，a=42.9，解此三角形．（精确到0.1cm）解:根据三角形的内角和定理：C=180º-(A+B)=66.2º由正弦定理可得429818801320ooasinB.sin.b.(cm)sinAsin.由正弦定理可得429662741320ooasinC.sin.c.(cm)sinAsin.应用正弦定理解三角形题型一：已知两角和任意一边，求出其他两边和一角三、例题讲解三、例题讲解解:由正弦定理可得28400899920obsinAsinsinB.a0180ooB64,oB当时C=180º-(A+B)≈76º(1)20763040ooasinCsinc(cm)sinAsinC=180º-(A+B)≈24º20241340ooasinCsinc(cm)sinAsin(2)当B≈116º时，例2.在△ABC中，a=20cm，b=28cm,A=40º，解此三角形．64oB116oB或题型二：已知两边和其中一边的对角，求另一边和另外两个角1.在△ABC中，已知c=10，A=45o，C=30o，则a=_____；2.在△ABC中，已知a=8，B=60o，C=75o，则b=_____；3.在△ABC中，C=2B，则（）A.B.C.D.sin3sinBBbaabcaac46B102四、练习四、练习一、正弦定理：二、可以用正弦定理解决的三角问题：题型一：知两角及一边，求其它的边和角题型二：知两边及其中一边对角，求其他边和角以及正弦定理的变形形式.五、小结五、小结abcsinAsinBsinC六、作业六、作业课本P10A组1、2