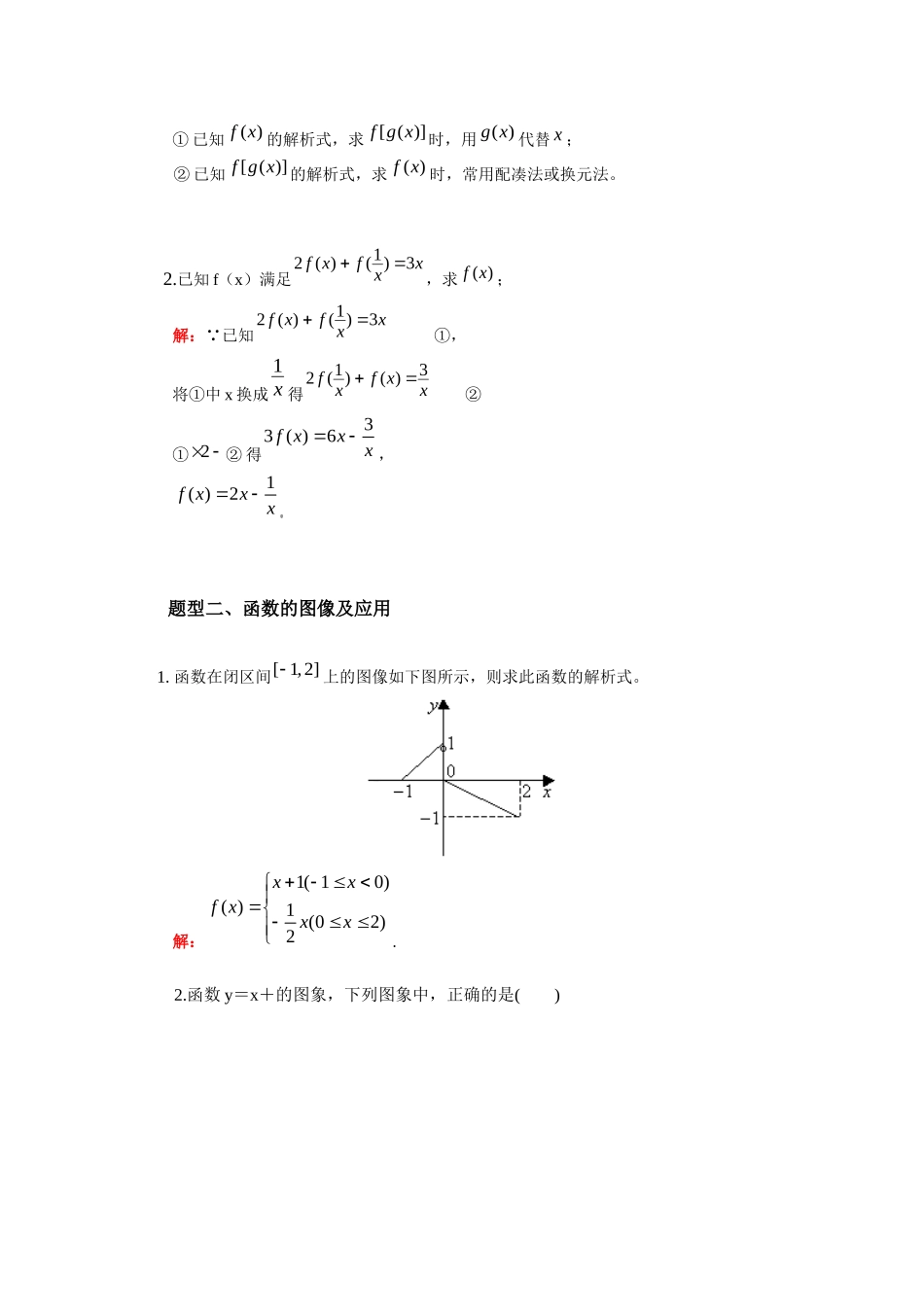
学习目标: (1)明确函数的三种表示方法; (2)会根据不同实际情境选择合适的方法表示函数; (3)通过具体实例,了解简单的分段函数及应用. 学习重点:函数的三种表示方法,分段函数的概念. 学习难点:分段函数的表示及其图象. 学习过程: 1、函数的表示方法: (1)解析法:用_____________表示两个变量之间的对应关系; 优缺点: (2)图像法:用_____________表示两个变量之间的对应关系; 优缺点: (3)列表法; 用_____________来表示两个变量之间的对应关系。 优缺点: 问题思考: 1、任何一个函数都可以用解析法表示吗? 2、函数的解析式与函数图像的关系是什么?题型一:求函数解析式1.(1)已知2( )43f xxx,求(1)f x ; (2)已知2(1)2f xxx,求( )f x . 解:(1)22(1)(1)4(1)32f xxxxx. (2)配凑法:2(1)(1)21 2f xxxx2(1)41xx2(1)4(1)3xx∴2( )43f xxx. 换元法:令1xt ,则1xt ,22( )(1)2(1)43f ttttt ∴ 2( )43f xxx. 说明:① 已知( )f x 的解析式,求[ ( )]f g x时,用 ( )g x 代替 x ;② 已知[ ( )]f g x的解析式,求( )f x 时,常用配凑法或换元法。 2.已知 f(x)满足xxfxf3)1()(2,求)(xf;解: 已知xxfxf3)1()(2 ①,将①中 x 换成 x1得xxfxf3)()1(2 ②① 2 ② 得33 ( )6f xxx,1( )2f xxx新疆源头学子小屋特级教师王新敞http://www.xjktyg.com/wxc/wxckt@126.comwxckt@126.comhttp://www.xjktyg.com/wxc/王新敞特级教师源头学子小屋新疆题型二、函数的图像及应用1. 函数在闭区间[ 1,2]上的图像如下图所示,则求此函数的解析式。 解:1( 10)( )1 (02)2xxf xxx .2.函数 y=x+的图象,下列图象中,正确的是( )高·考¥资%源~网【答案】 C题型三:有关分段函数的问题1.下列关于分段函数的叙述正确的有( )① 定义域是各段定义域的并集,值域是各段值域的并集;②尽管在定义域不同的部分有不同的对应法则,但它们是一个函数;③若 D1、D2分别是分段函数的两个不同对应法则的值域,则 D1∩D2=Ø.A.1 个 B.2 个C.3 个 D.0 个【解析】 ①②正确,③不正确,故选 B.【答案】 B2.设函数 f(x)=则 f(-4)=________,若 f(x0)=8,则 x0=...